Question

8．已知DE=CE，AC=AB，∠CED=∠CAB=90°，N是BD中点．
（1）如图1，求证：EN⊥AN，EN=AN；
（2）将△DCE绕C旋转至如图2位置，其他条件不变，试探究EN与AN的关系并证明；
（3）如图3，M是CD的中点，BE交AM于F，填空：$\frac{AM}{BE}$=$\frac{\sqrt{2}}{2}$．

Answer 1

分析 （1）如图1中，延长EN交AB于F．只要证明△EDN≌△FBN，△AEF是等腰三角形即可．
（2）结论：EN=AN，EN⊥AN．如图2中，延长EN到F，使得EN=NF，延长CA、BF交于点G，先证明△EDN≌△FBN，再证明△ACE≌△ABF，即可解决问题．
（3）结论：$\frac{AM}{BE}$=$\frac{\sqrt{2}}{2}$．作AN⊥BE，使得AN=BE，AN交BE于J，连接CN，NM，延长NM到H，使得MH=MN，连接HD、HE、AH、AE，延长NC交DE于G，延长AE交NG于O，延长DE到P．利用全等三角形的性质，想办法证明四边形EHAB是平行四边形，△ANH是等腰直角三角形即可．

解答 （1）证明：如图1中，延长EN交AB于F．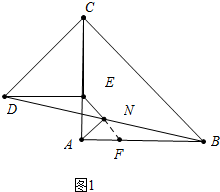

∵∠CED=∠CAB=90°，
∴DE⊥AC，AB⊥AC，
∴DE∥AB，
∴∠EDN=∠FBN，
在△EDN和△FBN中，
$\left\{\begin{array}{l}{∠EDN=∠FBN}\\{DN=BN}\\{∠DNE=∠BNF}\end{array}\right.$，
∴△EDN≌△FBN，
∴DE=FB=EC，EN=NF，
∵AC=AB，
∴AE=AF，∵EN=NF，
∴AN=EN=FN，AN⊥EF，
∴AN⊥EN，AN=EN．

（2）结论：EN=AN，EN⊥AN．
理由：如图2中，延长EN到F，使得EN=NF，延长CA、BF交于点G，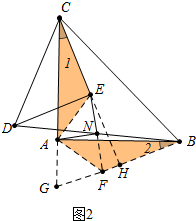

在△EDN和△FBN中，
$\left\{\begin{array}{l}{DN=BN}\\{∠DNE=∠BNF}\\{EN=NF}\end{array}\right.$，
∴△EDN≌△FBN，
∴DE=BF=CE，∠EDN=∠FBN，
∴DE∥BF，
∴∠CED=∠CHG=90°，
∴∠1+∠G=90°，∠2+∠G=90°，
∴∠1=∠2，
在△ACE和△ABF中，
$\left\{\begin{array}{l}{AC=AB}\\{∠1=∠2}\\{CE=BF}\end{array}\right.$，
∴△ACE≌△ABF，
∴AE=AF，∠CAE=∠BAF，
∴∠EAF=∠CAB=90°，
∵EN=NF，
∴AN⊥EF，AN=EN=NF，
∴EN=AN，EN⊥AN．

（3）如图3中，结论：$\frac{AM}{BE}$=$\frac{\sqrt{2}}{2}$．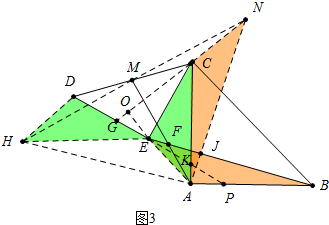

理由：作AN⊥BE，使得AN=BE，AN交BE于J，连接CN，NM，延长NM到H，使得MH=MN，连接HD、HE、AH、AE，延长NC交DE于G，延长AE交NG于O，延长DE到P．
∵∠CAN+∠BAN=90°，∠BAN+∠ABE=90°，
∴∠CAN=∠ABE，
∵AC=AB，AN=EB，
∴△CAN≌△ABE，
∴AE=CN，∠AEB=∠CNA，
∵∠AEB+∠EAJ=90°，
∴∠ANO+∠EAJ=90°，
∴∠NOA=90°，
∵∠EGO+∠OEC=90°，∠OEC+∠OCE=90°，
∴∠OCE=∠GEO=∠AEP，
∵DM=MC，∠DMH=∠NMC，NM=MH，
∴△DMH≌△CMN，
∴DH=CN，∠DHM=∠MNC，
∴DH∥NG，
∴∠HDE=∠DGC，
∵∠DGC=∠DEC+∠OCE=90°+∠OCE，
∴∠HDE=90°+∠OCE=90°+∠AEP=∠AEC，
∵DH=AE，DE=EC，
∴△DHE≌△EAC，
∴HE=AC=AB，∠HED=∠ECA，
∵∠ECA+∠EKC=90°，∠APK+∠AKP=90°，∠AKP=∠EKC，
∴∠ECK=∠APK=∠HED，
∴HE∥AB，
∴四边形HEBA是平行四边形，
∴AH=BE=AN，
∵AH=AN，AE=CN，HE=AC，
∴△ACN≌△HEA，
∴∠HAE=∠CNA，
∵∠ANC+∠NAO=90°，
∴∠HAE+∠NAO=90°，
∴∠HAN=90°，
∴△HAN是等腰直角三角形，
∵MH=MN，
∴AM=MN=MH，
∴△AHM，△AMN都是等腰直角三角形，
∴AN=$\sqrt{2}$AM，
∴BE=$\sqrt{2}$AM．
∴$\frac{AM}{BE}$=$\frac{\sqrt{2}}{2}$．
故答案为$\frac{\sqrt{2}}{2}$．

点评 本题考查几何变换综合题、全等三角形的判定和性质、等腰直角三角形的性质和判定、平行四边形的判定和性质等知识，解题的关键是灵活应用全等三角形的性质解决问题，学会添加辅助线，构造全等三角形，属于中考压轴题．