练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知关于x的多项式A，当A﹣（x﹣2）2=x（x+7）时．

    （1）求多项式A．

    （2）若2x2+3x+l=0，求多项式A的值．

    【答案】（1）A=2x2+3x+4；（2）多项式A的值为3．

    【解析】试题分析：（1）原式整理后，化简即可确定出A；

    （2）已知等式变形后代入计算即可求出A的值．

    试题解析：（1）A﹣（x﹣2）2=x（x+7），

    整理得：A=（x﹣2）2+x（x+7）=x2﹣4x+4+x2+7x=2x2+3x+4；

    （2）∵2x2+3x+1=0，

    ∴2x2+3x=﹣1，

    ∴A=﹣1+4=3，

    则多项式A的值为3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个多边形的内角和是它外角和的1.5倍，那么这个多边形是______边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】①（-3)+ 3=_____；②（+3)+5=_____； ③ -1+0=____ _；

    ④(-3)+(-2)= _____ ⑤ 4+（-7）=_____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是

    A、2x+3y=5xy B、5m2·m3=5m5 C、（a—b）2=a2—b2 D、m2·m3=m6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为满足消费者需要，红星厂一月份生产手提电脑200台，计划二、三月份共生产2500台．设二、三月份每月的平均增长率为x，根据题意列出的方程是（　　）

    A. 200（1+x）2=2500 B. 200（1+x）+200（1+x）2=2500

    C. 200（1﹣x）2=2500 D. 200+200（1+x）+2000（1+x）2=250

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解学生的课余生活，某中学在全校范围内随机抽取部分学生进行问卷调查，问卷中请学生选择最喜欢的课余生活种类（每人只选一类），选项有音乐类、美术类、体育类及其他共四类．调查后将数据绘制成扇形统计图和条形统计图（如图所示）．

    （1）请根据所给的扇形图和条形图，直接填写出扇形图中缺失的数据，并把条形图补充完整；

    （2）在扇形统计图中，音乐类选项所在的扇形的圆心角的大小为 °；

    （3）这所中学共有学生1200人，求喜欢音乐和美术类的课余生活共有多少人？

    （4）在问卷调查中，小丁和小李分别选择了音乐类和美术类，校学生会要从选择音乐类和美术类的学生中分别抽取一名学生参加活动，用列表或画树状图的方法求小丁和小李恰好都被选中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果－b是a的立方根，则下列结论正确的是（ ）

    A. －b＝a B. －b＝a C. b＝a D. b＝a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果a，b互为相反数，那么（6a2﹣12a）﹣6（a2+2b﹣5）的值为（ ）

    A. ﹣18

    B. 18

    C. 30

    D. ﹣30

    查看答案和解析>>

    科目：初中数学 来源： 题型：

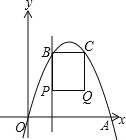
    【题目】如图，在平面直角坐标系中，经过原点的抛物线y=-x2+4mx（m＞0）与x轴的另一个交点为点A，过点P（1，m）作直线PB⊥x轴，交抛物线于点B，作点B关于抛物线对称轴的对称点C（点B、C不重合），连结BC，当点P、B不重合时，以BP、BC为边作矩形PBCQ，设矩形PBCQ的周长为l．

    （1）当m=1时，求点A的坐标．

    （2）当BC=时，求这条抛物线所对应的函数表达式．

    （3）当点P在点B下方时，求l与m之间的函数关系．

    （4）连结CP，以CP为直角边作等腰直角三角形PCM，直接写出点M落在坐标轴上时m的值．

    查看答案和解析>>

    同步练习册答案