Question

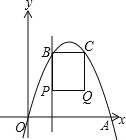
【题目】如图，在平面直角坐标系中，经过原点的抛物线y=-x2+4mx（m＞0）与x轴的另一个交点为点A，过点P（1，m）作直线PB⊥x轴，交抛物线于点B，作点B关于抛物线对称轴的对称点C（点B、C不重合），连结BC，当点P、B不重合时，以BP、BC为边作矩形PBCQ，设矩形PBCQ的周长为l．

（1）当m=1时，求点A的坐标．

（2）当BC=时，求这条抛物线所对应的函数表达式．

（3）当点P在点B下方时，求l与m之间的函数关系．

（4）连结CP，以CP为直角边作等腰直角三角形PCM，直接写出点M落在坐标轴上时m的值．

Answer 1

【答案】(1) （4，0）；(2) y=-x2+x或y=-x2+x．（3）l=-2m+2．（4）m=，m=．

【解析】

试题分析：（1）根据自变量与函数值的对应关系，可得答案；

（2）根据BC的长，可得关于m的方程，根据解方程，可得m的值；

（3）根据周长公式，可得答案；

（4）利用直线PC的斜率求出直线PE的斜率，并求出直线PE的参数方程，讨论点E在x轴与y轴的情况，并分别求出点E的参数坐标，根据PC=PE，利用两点间距离公式求解．此题也可用开锁法进行求解．

试题解析：（1）当m=1时，抛物线的解析式为y=-x2+4x．

当y=0时，-x2+4x=0，解得x1=0，x2=4，即A点坐标为（4，0）；

（2）当y=-x2+4mx中x=1时，y=4m-1，B（1，4m-1）．且抛物线的对称轴为x=-=2m．

当点B在对称轴左侧时，即m＞时，BC=2（2m-1）=4m-2．

当BC=时，4m-2=．m=，这条抛物线的解析式为y=-x2+x．

当BC=时，2-4m=．m=，这条抛物线的解析式为y=-x2+x．

（3）当点B在对称轴左侧，同时点P在点B的下方，即＜m＜时，

l=2[2（1-2m）+（4m-1-m）]，l=-2m+2．

（4）分三种情况：P在对称轴左侧，P（1，m），B（1，4m-1），C（4m-1，4m-1），

BC=4m-2，BP=3m-1，

①若∠CPQ=90°，PC=PQ，如图1，

此时，△CBP≌△PFQ，

∴CB=PF，即4m-2=m，解得m=，

②若∠PCQ=90°，CP=CQ，如图2，

此时，△QFP≌△CDQ，

∴DF=CD，即4m-1=4m-1，方程无解；

∴此种情况不成立．

③如图3，

B（1，4m-1），P（1，m），C（4m-1，4m-1），

若∠CPQ=90°，PC=PQ，△CBP≌△QFC，

BP=CF，即3m-1=4m-1，解得m=0（舍），

④如图4，

∠CQP=90°，CQ=CP，

△CBP≌△PFQ，

BP=QF，即4m-1-m=1，解得m=；

⑤如图5，

∠CQP=90°，CQ=CP，

△CBP≌△PFQ，

BC=PF，即2-4m=m，解得m=；

综上所述：m=，m=．