
解:(1)将k=2,m=3代入得:反比例解析式为y=

,M(3,3),
∵MA⊥x轴,MB⊥y轴,
∴E的横坐标为3,F纵坐标为3,
代入反比例解析式得:E(3,

),F(

,3),
设直线EF解析式为y=kx+b,
将E与F坐标代入得:

,
解得:
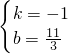
,
则直线EF解析式为y=-x+

;
(2)连接OM,EF,OE,OM与EF交于点C,
∵M(m,m),反比例解析式为y=

,
∴E(m,

),F(

,m),即E与F关于y=x对称,四边形AOBM为正方形,
∵∠BOF=22.5°,
∴∠BOF=∠COF=∠EOC=∠AOE=22.5°,
由对称性得到∠FCO=∠ECO=90°,
在△BOF和△AOE中,
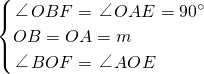
,
∴△BOF≌△AOE(ASA),
同理△BOF≌△COF,△COF≌△AOE,
∴BF=AE=

,
又BM=AM=m,
∴S
△BOF=

m•

=

k,
∴S
五边形BOAEF=4S
△BOF=2k=2,
则k=1.
分析:(1)将k的值代入确定出反比例解析式,将m的值代入确定出M坐标,根据图形得到E的横坐标与F的纵坐标都为3,代入反比例解析式中确定出E与F坐标,设直线EF解析式为y=kx+b,将E与F坐标代入求出k与b的值,即可确定出直线EF的解析式;
(2)连接EF,OM,OE,由M横纵坐标相等得到四边形AOBM为正方形,由正方形的性质及∠BOF=22.5°,得到三角形BOF、三角形FCO、三角形ECO及三角形AOE全等,三角形BOF的面积等于|k|的一半,表示出四个面积之和,即为五边形BOAEF的面积,根据五边形的面积为2列出关于k的方程,求出方程的解即可得到k的值.
点评:此题考查了反比例函数综合题,涉及的知识有:正方形的判定与性质,全等三角形的判定与性质,反比例函数k的几何意义,坐标与图形性质,以及待定系数法求一次函数解析式,灵活运用待定系数法是解本题第一问的关键.

 (k>0),过点M(m,m)(m>
(k>0),过点M(m,m)(m> )作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y=
)作MA⊥x轴,MB⊥y轴,垂足分别是A和B,MA、MB分别交双曲线y= (k>0)于点E、F.
(k>0)于点E、F. 解:(1)将k=2,m=3代入得:反比例解析式为y=
解:(1)将k=2,m=3代入得:反比例解析式为y= ,M(3,3),
,M(3,3), ),F(
),F( ,3),
,3), ,
,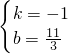 ,
, ;
; ,
, ),F(
),F( ,m),即E与F关于y=x对称,四边形AOBM为正方形,
,m),即E与F关于y=x对称,四边形AOBM为正方形,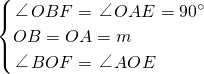 ,
, ,
, m•
m• =
= k,
k,

 阅读快车系列答案
阅读快车系列答案