
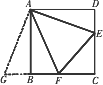
如下图所示,在正方形ABCD中,点E、F分别在DC、BC边上,∠EAF=45°.那么BF+DE与EF相等吗?为什么?
|
分析:延长FB到点G,使得BG=DE,则GF=BF+DE.要说明BF+DE与EF相等,只需证明EF=GF即可,可考虑通过证明△AFE≌△AFG来证明EF=GF. 解:BF+DE=EF. 证明:延长FB到点G,使得BG=DE. 因为四边形ABCD为正方形, 所以AD=AB,∠D=∠ABG=90°. 因为BG=DE, 所以Rt△ADE≌Rt△ABG(SAS). 所以AG=AE,∠DAE=∠BAG. 所以∠EAG=∠DAB=90°. 因为∠EAF=45°, 所以∠FAE=∠FAG 因为AF=AF, 所以△EAF≌△GAF(SAS) 所以GF=EF. 所以BF+DE=BF+BG=GF=EF. 点评:一般题目要求证明形如“A+B=C”型的结论的时候,有两种思路,思路一:找到一条线段D,使得D=A+B,然后证明D=C;思路二:将C拆分为两条线段的和,如C=D+E,然后分别证明A=D和B=E即可. |


科目:初中数学 来源:2013届广西大学附属中学九年级10月月考数学试卷(带解析) 题型:解答题
已知:如下图所示,在正方形ABCD中,P是BC上的点,且BP=3PC, Q是CD的中点.ΔADQ与ΔQCP是否相似?为什么?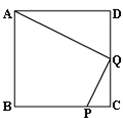
查看答案和解析>>
科目:初中数学 来源:2012-2013学年广西大学附属中学九年级10月月考数学试卷(解析版) 题型:解答题
已知:如下图所示,在正方形ABCD中,P是BC上的点,且BP=3PC, Q是CD的中点.ΔADQ与ΔQCP是否相似?为什么?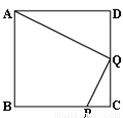
查看答案和解析>>
科目:初中数学 来源:专项题 题型:解答题



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com