
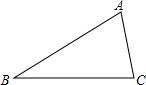
 已知:如图,△ABC中.
已知:如图,△ABC中.分析 (1)分别作∠ABC和∠ACB的平分线,两平分线相交于点O,再过点O作OH⊥BC于H,然后以点O为圆心,OH为半径作圆,则⊙O为△ABC的内切圆;
(2)作OQ⊥AB于Q,OP⊥DE于P,如图,利用切线长定理得到EQ=EP,DP=DH,BQ=BH,由于BE+BD+DP+EP=20,利用等线段代换得到BE+BD+DH+EQ=20,则BQ+BH=20,所以BQ=BH=10.
解答 解:(1)如图,⊙O为所作;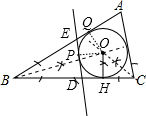
(2)作OQ⊥AB于Q,OP⊥DE于P,如图,
∵⊙O为△ABC的内切圆,
∴点P、Q为切点,
∵DE为⊙O的切线,
∴P点为切点,
∴EQ=EP,DP=DH,BQ=BH,
∵△BDE的周长为20,
∴BE+BD+DP+EP=20,
∴BE+BD+DH+EQ=20,
即BQ+BH=20,
∴BQ=BH=10,
即点B到圆O的切线长为10.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线长定理.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:解答题
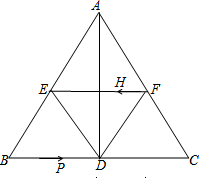 如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
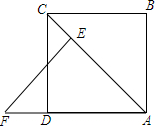 如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置
如图,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
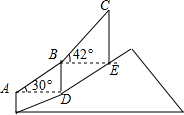 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com