
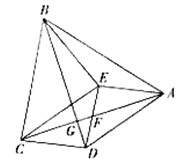
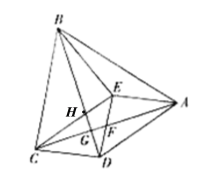
【题目】如图,四边形ABCD内一点E满足EB=EC,EA=ED,∠BEC=∠AED=90°,AC交DE于点F,交BD于点G.
(1)∠AGB的度数为
(2)若四边形AECD是平行四边形
①求证:AC=AB
②若AE=2,求AF·CG的值
【答案】(1)90°;(2)①见解析,②AFCG= 4.
【解析】
(1)先利用SAS证明△BED≌△CEA,得∠DBE=∠ACE,由∠BHE=∠CHG,得到∠HGC=∠BEH=90°,从而∠AGB=90°;
(2)①由(1)可知△BED≌△CEA,得BD=CA,由平行四边形AECD,得AE=CD=DE,∠AED=∠EDC=90°,从而∠CED=45°,∠BED=135°,利用周角得到∠BEA=135°,可证△BAE≌△BDE,得到BD=BA,从而AC=AB;
②由①可知,△CAE≌△BAE,得∠BAE=∠EAC=∠BDE,由∠EAC+∠AFE=90°,∠GFD=∠AFE,得∠GFD+∠BDE=90°,从而∠CGD=90°,可证△CGD∽△AEF,根据相似三角形的性质得到![]() =
=![]() ,由AE=4,从而得解.
,由AE=4,从而得解.
解:(1)∵∠BEC=∠AED=90°,
∴∠BED=∠CEA,
又∵BE=EC,EA=ED,
∴△BED≌△CEA,
∴∠DBE=∠ACE,
又∵∠BHE=∠CHG,
∴∠HGC=∠BEH=90°,
∴∠AGB=90°;
(2)①∵四边形AECD是平行四边形,
∴∠AED=∠EDC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=ED,∴ED=CD,
∴∠CED=45°,
∴∠BED=90°+45°=135°,
∵∠AED=∠BEC=90°,
∴∠AEB=360°-90°-90°-45°=135°,又EB=EB,ED=EA,
∴△BAE≌△BDE(SAS),
∴DB=AB;
∵∠BEC=∠AED=90°,
∴∠BED=∠CEA,
∵EB=EC,EA=ED,
∴△BED≌△CEA,
∴BD=CA,
∴AC=AB.
②∵△BAE≌△BDE,
∴△CAE≌△BAE,
∴∠BAE=∠CAE=∠BDE,
∵∠EAF+∠AFE=90°,
∴∠AFE+∠BAE=90°,
∵∠GFD=∠AFE,∠EDB=∠EAB,
∴∠EDB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△AEF,
∴![]() =
=![]() ,
,
∴AFCG=CDAE=4.
故答案为(1)90°;(2)①见解析,②4.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
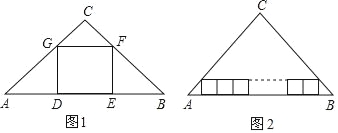
【题目】在△ABC中,∠C=90°,AC=4,BC=3,如图1,四边形DEFG为△ABC的内接正方形,则正方形DEFG的边长为_____.如图2,若三角形ABC内有并排的n个全等的正方形,它们组成的矩形内接于△ABC,则正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一驴友分三次从![]() 地出发沿着不同线路(
地出发沿着不同线路(![]() 线、
线、![]() 线、
线、![]() 线)去
线)去![]() 地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;
地,在每条线路上行进的方式都分为穿越丛林、涉水行走和攀登这三种.他涉水行走4小时的路程与攀登6小时的路程相等;![]() 线、
线、![]() 线路程相等,都比
线路程相等,都比![]() 线路程多
线路程多![]() ;
;![]() 线总时间等于
线总时间等于![]() 线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完
线总时间的一半;他用了3小时穿越丛林、2小时涉水行走和2小时攀登走完![]() 线;在
线;在![]() 线中穿越丛林、涉水行走和攀登所用时间分别比
线中穿越丛林、涉水行走和攀登所用时间分别比![]() 线上升了
线上升了![]() .若他用了
.若他用了![]() 小时穿越丛林、
小时穿越丛林、![]() 小时涉水行走和
小时涉水行走和![]() 小时攀登走完
小时攀登走完![]() 线,且
线,且![]() 都为正整数,则
都为正整数,则![]() _____.
_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用![]() (元)与种植面积
(元)与种植面积![]() 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
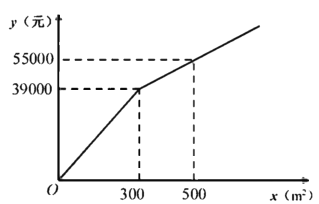
(1)直接写出当![]() 和
和![]() 时,
时,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共![]() ,若甲种花卉的种植面积不少于
,若甲种花卉的种植面积不少于![]() ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
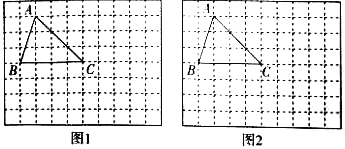
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中有格点△ABC(注:顶点在网格线交点处的三角形叫做格点三角形).只用没有刻度的直尺,按如下要求画图,
(1)以点C为位似中心,在如图中作△DEC∽ABC,且相似比为1:2;
(2)若点B为原点,点C(4,0),请在如图中画出平面直角坐标系,作出△ABC的外心,并直接写出△ABC的外心的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是作一个角的角平分线的方法:以![]() 的顶点
的顶点![]() 为圆心,以任意长为半径画弧,分别交
为圆心,以任意长为半径画弧,分别交![]() 于
于![]() 两点,再分别以
两点,再分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作画弧,两条弧交于点
长为半径作画弧,两条弧交于点![]() ,作射线
,作射线![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.

(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )

A、3或4![]() B、4或3
B、4或3![]() C、3或4 D、3
C、3或4 D、3![]() 或4
或4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com