
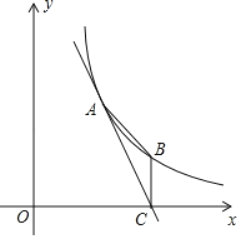
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线交反比例函数图象于点B.
(1)求反比例函数和直线AC的解析式;
(2)求△ABC的面积;
(3)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,请直接写出符合条件的所有D点的坐标.
【答案】(1)y=![]() ;y=﹣
;y=﹣![]() x+8;(2)B(6,2);△ABC的面积=3;(3)(3,2)或(3,6)或(9,﹣2).
x+8;(2)B(6,2);△ABC的面积=3;(3)(3,2)或(3,6)或(9,﹣2).
【解析】
(1)把点A的坐标代入反比例函数即可求出k,再把点A和点C的坐标代入一次函数中即可求出解析式;
(2)由题意BC⊥x轴,且点B在反比例函数上,可求出点B的坐标,从而求出△ABC的面积;
(3)根据平行四边形的性质求得点D的坐标,注意分三种情况讨论.
解:(1)把点A(3,4)代入y=![]() (x>0),得
(x>0),得
k=xy=3×4=12,
故该反比例函数解析式为:y=![]() ;
;
把A(3,4),C(6,0)代入y=mx+n中,
可得:![]() ,
,
解得: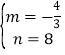 ,
,
所以直线AC的解析式为:y=﹣![]() x+8;
x+8;
(2)∵点C(6,0),BC⊥x轴,
∴把x=6代入反比例函数y=![]() ,得
,得
y=![]() =2.
=2.
则B(6,2).
所以△ABC的面积=![]() ;
;
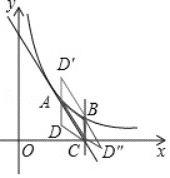
(3)①如图,当四边形ABCD为平行四边形时,AD∥BC且AD=BC,
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yA﹣yD=yB﹣yC即4﹣yD=2﹣0,故yD=2,
所以D(3,2);
②如图,当四边形ACBD′为平行四边形时,AD′∥CB且AD′=CB,
∵A(3,4)、B(6,2)、C(6,0),
∴点D的横坐标为3,yD′﹣yA=yB﹣yC即yD﹣4=2﹣0,故yD′=6.
所以D′(3,6).
③如图,当四边形ACD″B为平行四边形时,AC=BD″且AC∥BD″.
∵A(3,4)、B(6,2)、C(6,0),
∴xD″﹣xB=xC﹣xA即xD″﹣6=6﹣3,故xD″=9.
yD″﹣yB=yC﹣yA即yD″﹣2=0﹣4,故yD″=﹣2.
所以D″(9,﹣2).
综上所述,符合条件的点D的坐标是:(3,2)或(3,6)或(9,﹣2).


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装专卖店又缺少资金![]() “中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务
“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务![]() 所有债务均不计利息
所有债务均不计利息![]() 已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量
已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量![]() 件
件![]() 与销售价
与销售价![]() 元
元![]() 件
件![]() 之间的关系可用图中的一条折线
之间的关系可用图中的一条折线![]() 实线
实线![]() 来表示
来表示![]() 该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元
该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元![]() 不包含债务
不包含债务![]() .
.
![]() 求日销售量
求日销售量![]() 件
件![]() 与销售价
与销售价![]() 元
元![]() 件
件![]() 之间的函数关系式;
之间的函数关系式;
![]() 若该店暂不考虑偿还债务,当某天的销售价为48元
若该店暂不考虑偿还债务,当某天的销售价为48元![]() 件时,当天正好收支平衡
件时,当天正好收支平衡![]() 收人
收人![]() 支出
支出![]() ,求该店员工的人数;
,求该店员工的人数;
![]() 若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?
若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知RtΔABC,∠C=90°,D为BC的中点.以AC为直径的圆O交AB于点E.
(1)求证:DE是圆O的切线.
(2)若AE:EB=1:2,BC=6,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为AB中点,BC=4BF,那么图中与△ADE相似的三角形有( )
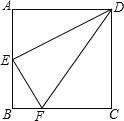
A. △CDFB. △BEFC. △BEF、△DCFD. △BEF,△EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
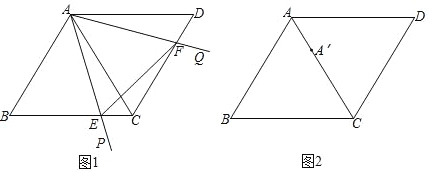
【题目】如图1,AC是边长为6的菱形ABCD的对角线,∠ABC=∠PAQ=60°,∠PAQ绕点A旋转,射线AP、AQ分别交边BC、CD于点E、F,连接EF.请探究:
(1)在旋转过程中,线段AE、AF有怎样的数量关系?并说明理由;
(2)在旋转过程中,△AEF的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由
(3)如图2,将∠PAQ沿着AC向下平移至点A处,使CA′:AA′=2:1,在∠PA′Q绕点A′旋转过程中,始终保持∠ABC=∠PA′Q,射线A′P、A′Q分别交直线BC、CD于点E、F,连接EF.当S△A′EF:S菱形ABCD=19:18时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
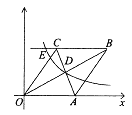
【题目】已知:如图在直角坐标系中,有菱形![]() ,
, ![]() 点的坐标为
点的坐标为![]() ,对角线
,对角线![]() ,
, ![]() 相交于
相交于![]() 点,双曲线
点,双曲线![]() 经过
经过![]() 点,交
点,交![]() 的延长线于
的延长线于![]() 点,且
点,且![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
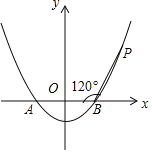
【题目】如图,已知抛物线![]() 与x轴相交于A,B两点,点P是抛物线上一点,且
与x轴相交于A,B两点,点P是抛物线上一点,且![]() ,
,![]() .
.
![]() 求该抛物线的表达式;
求该抛物线的表达式;
![]() 设点
设点![]() 为抛物线上的一个动点,当点M在曲线BA之间
为抛物线上的一个动点,当点M在曲线BA之间![]() 含端点
含端点![]() 移动时,求
移动时,求![]() 的最大值及取得最大值时点M的坐标.
的最大值及取得最大值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.
(1)求证:DF是⊙O的切线;
(2)若CF=1,DF=![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com