
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F: ![]() 与直线x=-2交于点P.
与直线x=-2交于点P.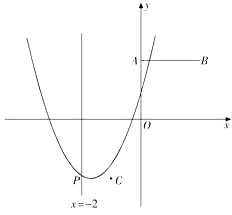
(1)当抛物线F经过点C时,求它的表达式;
(2)抛物线F上有两点M ![]() 、N
、N ![]() ,若-2≤
,若-2≤ ![]() ,
, ![]() <
< ![]() ,求m的取值范围;
,求m的取值范围;
(3)设点P的纵坐标为 ![]() ,求
,求 ![]() 的最小值,此时抛物线F上有两点M
的最小值,此时抛物线F上有两点M ![]() 、N
、N ![]() ,
,
若 ![]() ≤-2,比较
≤-2,比较 ![]() 与
与 ![]() 的大小;
的大小;
(4)当抛物线F与线段AB有公共点时,直接写出m的取值范围。
【答案】
(1)
解:∵抛物线F经过点C(-1,-2),
∴ ![]() .
.
∴m=-1.
∴抛物线F的表达式是 ![]()
(2)
解:抛物线F的对称轴为:直线x=m,
当x≥m时,y随x的增大而增大;
点M、N均在直线x=-2的右侧,
∴直线x=-2必须在直线x=m右侧或与之重合
∴m≤-2
(3)
解:方法一:当x=-2时, ![]() =
= ![]() .
.
∴当m=-2时, ![]() 的最小值=-2.
的最小值=-2.
此时抛物线F的表达式是 ![]() .
.
∴当 ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
∵ ![]() ≤-2,
≤-2,
∴ ![]() >
> ![]() .
.
方法二:当直线x=-2与抛物线F的对称轴(直线x=m)重合时,
![]() 有最小值,此时m=-2
有最小值,此时m=-2
此时抛物线F的表达式是 ![]() .
.
∴当 ![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
∵ ![]() ≤-2,
≤-2,
∴ ![]() >
> ![]() .
.
(4)![]()
或 ![]() .
.
【解析】(4)解:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),
∴![]() 或
或![]() ,
,
解得:-2≤m≤0或2 ≤ m ≤ 4 .
所以答案是:-2≤m≤0或2 ≤ m ≤ 4 .
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.
(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
(3)若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M落在矩形ABCD外部时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣a(x﹣m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点.
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于D点.
①当△ABC的面积为1时,求a的值.
②当△ABC的面积与△ABD的面积相等时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个结论:
①a÷m+a÷n=a÷(m+n);
② 某商品单价为a元。甲商店连续降价两次,每次都降10%。乙商店直接降20%。顾客选择甲或乙商店购买同样数量的此商品时,获得的优惠是相同的;
③若 ![]() ,则
,则 ![]() 的值为
的值为 ![]() ;
;
④关于x分式方程 ![]() 的解为正数,则
的解为正数,则 ![]() >1。
>1。
请在正确结论的题号后的空格里填“正确” ,在错误结论的题号后空格里填“错误”:
①; ②; ③; ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AC=2 ![]() ,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为 .
,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;
②3b+c+6=0;
③当x2+bx+c> ![]() 时,x>2;
时,x>2;
④当1<x<3时,x2+(b﹣1)x+c<0,
其中正确的序号是( )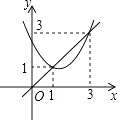
A.①②④
B.②③④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲转盘被分成 3 个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转,直到指针指向一个区域为止). 
(1)请你用画树状图或列表格的方法,求点(x,y)落在第二象限内的概率;
(2)直接写出点(x,y)落在函数y=﹣ ![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com