
【题目】如图1,在平面直角坐标系中,△OAB是等边三角形,O为坐标原点,点A的坐标是(3,0),点C在OA上且OC=1,连接BC.一动点P从点A出发,沿折线A→B→O的方向向终点O运动,记点P移动的路程为m.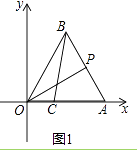
(1)当点P在线段AB上运动时,连接OP,求满足△BPO≌△OCB的m值;
(2)连接PC,求△OPC的面积s关于m的函数表达式;
(3)如图2,过点P作边AB的垂线l,并以直线l为对称轴,作线段AC的对称线段A1C1 . 请写出在点P的运动过程中,线段A1C1与y轴有交点时m的取值范围.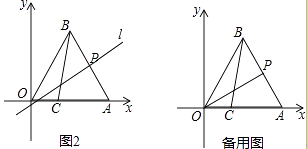
【答案】
(1)
解:∵△BPO≌△OCB,
∴BP=OC=1.
∴m=AB﹣BP=3﹣1=2
(2)
解:①如图1所示:当点P在AB上运动时,过点P作PD⊥OA.
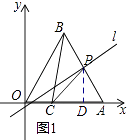
∵∠OAP=60°,∠PDA=90°,
∴∠APD=30°.
∴PD= ![]() PA
PA ![]() m.
m.
∴S= ![]() ×1×
×1× ![]() m=
m= ![]() m;
m;
②如图2所示:当点P在OB上时,过点P作PD⊥OA.
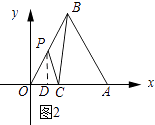
∵OP=AB+OB﹣m=6﹣m,
∴PD= ![]() (6﹣m),
(6﹣m),
∴S= ![]() ×1×
×1× ![]() (6﹣m)=
(6﹣m)= ![]() (6﹣m).
(6﹣m).
综上所述,S与m的函数关系式为S= 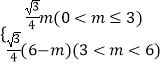
(3)
解:如图3所示:当点C的对应点C′落在y轴上时.
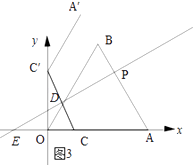
由翻折的性质可知:CC′⊥PE,DC=DC′,
又∵PE⊥AB,
∴DC∥PA.
∴∠C′CO=∠A=60°.
∴∠CC′O=30°.
∴CC′=2OC=2.
∴DC=1.
∵在△DCE中,∠EDC=90°,∠DCE=60°,
∴∠DEC=30°.
∴EC=2DC=2.
∴EC=CA.
∵DC∥AB,
∴ ![]() =
= ![]() .
.
∴AP=2.即m=2.
如图4所示:当点A的对称点A′在y轴上时.
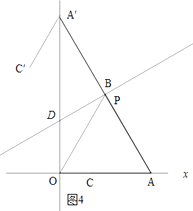
∵点A与点A′关于直线PD对称,
∴PA=PA′.
∵∠A=60°,∠AOA′=90°,
∴∠AA′O=30°.
∴AA′=2OA=6.
∴PA=3.
∴点B与点P重合,此时m=3.
如图5所示:当点P在OB上,点C′在y轴上.
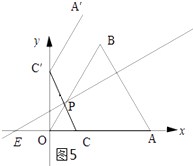
∵∠PCO=60°,∠POC=60°,
∴△OPC为等边三角形.
∴PO=OC=1.
∴PB=2.
∴m=PB+AB=5.
∴线段A1C1与y轴有交点时m的取值范围是2≤m≤5
【解析】(1)由全等三角形的性质可知BP=OC,由m=AB﹣PB求解即可;(2)过点P作PD⊥OA,垂足为D,三角形OPC的面积S= ![]() OCDP,然后分为点P在AB和OB上两种情况求得PD的长,从而得到S与m的函数关系式;(3)求得点A′或点C′恰好在y轴上时m的值,从而可确定出m的范围.
OCDP,然后分为点P在AB和OB上两种情况求得PD的长,从而得到S与m的函数关系式;(3)求得点A′或点C′恰好在y轴上时m的值,从而可确定出m的范围.
【考点精析】解答此题的关键在于理解两点间的距离的相关知识,掌握同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记.


科目:初中数学 来源: 题型:
【题目】下面是一名学生所做的4道练习题:①﹣22=4②a3+a3=a6③4m﹣4= ![]() ④(xy2)3=x3y6 , 他做对的个数( )
④(xy2)3=x3y6 , 他做对的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从地面竖直向上抛出一小球,小球离地面的高度h(米)与小球运动时间t(秒)之间关系是h=30t﹣5t2(0≤t≤6),则小球从抛出后运动4秒共运动的路径长是________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一探究活动:如图1,有甲、乙两个三角形,甲三角形内角分别为10°,20°,150°;乙三角形内角分别为80°,25°,75°.你能把每一个三角形分成两个等腰三角形吗?画一画,并标出每个等腰三角形顶角的度数. 
(1)小明按要求画出了图1中甲图的分割线,请你帮他作出图1中乙图的分割线;
(2)小明进一步探究发现:能将一个顶角为108°的等腰三角形分成三个等腰三角形;请在图2中用两种不同的方法画出分割线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种方法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月份,某品牌衬衣正式上市销售,3 月1日的销售量为10件,3月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到3月31日销售量为0,设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示。
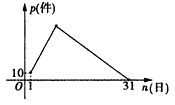
(1)求3月 日时,日销售量最大.
(2)写出p关于n的函数关系式(注明n 的取值范围);
(3)经研究表明,该品牌衬衣的日销量超过150件的时间为该品牌衬衣的流行期,请问:该品牌衬衣本月在市面的流行期是多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代有不少世界领先的数学研究成果是以华人数学家命名的,如:有一位数学家的关于完整三角和研究成果被国际数学界称为“华氏定理”,这是以________的姓氏命名的;另一位数学家在仿射微分几何学方面的研究成果在国际上被命为“苏氏锥面”,这是以________的姓氏命名的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com