
����Ŀ����ͼ��AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC������P�ӵ�A��������3cm/s���ٶ������˶��������B���������أ���3cm/s���ٶ������˶�������Q�ӵ�C��������1cm/s���ٶ������˶���������ͬʱ�������˶�ʱ��Ϊts������P���Q�ڶ����غ�ʱ��P��Q����ֹͣ�˶���
��1��AC=__cm��BC=__cm��
��2����tΪ��ֵʱ��AP=PQ��
��3����tΪ��ֵʱ��PQ=1cm��

���𰸡� 4 8
�������������������1������AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC����AC+BC=3AC=AB=12cm�����˼�����⣻
��2���ֱ��ʾ��AP��PQ��Ȼ����ݵ�����ϵAP=PQ�г�������⼴�ɣ�
��3��������ǰ���������Լ�����B�㷵�غ����1cm��������г�������⼴�ɣ�
�����������1����AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC��
��AC+BC=3AC=AB=12cm��
��AC=4cm��BC=8cm��
��2���������֪��AP=3t��PQ=4����3t��t����
��3t=4����3t��t����
��ã�t=![]() ��
��
�𣺵�t=![]() ʱ��AP=PQ��
ʱ��AP=PQ��
��3���ߵ�P��Q����·��Ϊ1cm��
����4+t����3t=1������ǰ����3t����4+t��=1����һ��������
���t=![]() ��t=
��t=![]() ��
��
������B��ʱ����һ���������P��Q����·��Ϊ1cm��
3t+4+t=12+12��1
��ã�t=![]() ��
��
�𣺵�tΪ![]() ��
�� ![]() ��
�� ![]() ʱ��PQ=1cm��
ʱ��PQ=1cm��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
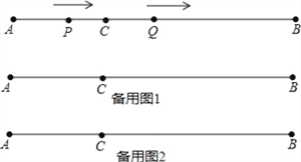
����Ŀ���ı���ABCD�����Σ��Խ���AC=8cm��BD=6cm��DH��AB��H����DH�ij��� 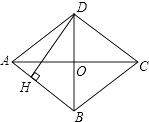
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������8�֣���ͼ��ij��ѧ¥AB�ĺ�����һ������CD�������������ļн���22��ʱ����ѧ¥�ڽ������ǽ�����¸�2m��Ӱ��CE���������������ļн���45��ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C�ľ���Ϊ18m (B��F��C��һ��ֱ����).
���ѧ¥AB�ĸ߶�.���������������
���������sin22��![]() 0.37��cos22��
0.37��cos22��![]() 0.93��tan22��
0.93��tan22��![]() 0.40 .��
0.40 .��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
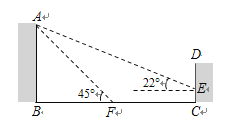
����Ŀ����֪����ͼ���ڡ�ABC�У�M�DZ�AB���е㣬D�DZ�BC�ӳ����ϵ�һ�㣬��CD= ![]() BC����DN��CM��AC�ڵ�N����֤���ı���MCDN��ƽ���ı��Σ�
BC����DN��CM��AC�ڵ�N����֤���ı���MCDN��ƽ���ı��Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB��y=kx��2��y���ཻ�ڵ�A���뷴��������y= ![]() �ڵ�һ�����ڵ�ͼ���ཻ�ڵ�B��m��2����
�ڵ�һ�����ڵ�ͼ���ཻ�ڵ�B��m��2���� 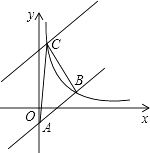
��1����ֱ��AB�ı���ʽ��
��2����ֱ��AB����ƽ�ƺ��뷴��������ͼ���ڵ�һ�����ڽ��ڵ�C���ҡ�ABC�����Ϊ18����ƽ�ƺ��ֱ�ߵı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ĸ����������ˮ��Ϊ60900�֣�����60900�ÿ�ѧ��������ʾΪ��������
A. 0.609��105 B. 6.09��104 C. 60.9��103 D. 609��102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ۺ�ʵ�����ϣ�С������С��Ҫ����һ���ӵĿ��ȣ���ͼ���Ӱ�EF��MN��С���ںӰ�MN�ϵ�A���ò���Dz�úӶ�С��Cλ�ڶ�������Ȼ���غӰ�����30�ף�����B������úӶ����߸�Dλ�ڱ�ƫ��30�㷽��ʱ������ͬѧ���CD=10�ף��������Щ��������ӵĿ��ȣ�����ȷ��0.1�����ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.132��
��1.132��
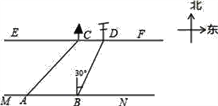
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ�߱�������ֱ�����أ�����1���2 ��ͬ���ڽǣ��ҡ�1=70���� ( )
A. ��2=70B. ��2=110
C. ��2=70���2=110D. ��2�Ķ�������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BD�Ǿ���ABCD�ĶԽ��ߣ� 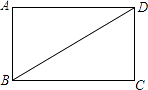
��1����ֱ�ߺ�Բ�����߶�BD�Ĵ�ֱƽ���ߣ��ֱ�AD��BC��E��F��������ͼ�ۼ�����д������֤������
��2������BE��DF�����ı���BEDF��ʲô�ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com