
【题目】如图,已知BD是矩形ABCD的对角线. 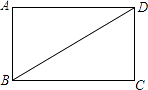
(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
【答案】
(1)解:如图所示,EF为所求直线;
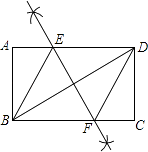
(2)解:四边形BEDF为菱形,理由为:
证明:∵EF垂直平分BD,
∴BE=DE,∠DEF=∠BEF,
∵AD∥BC,
∴∠DEF=∠BFE,
∴∠BEF=∠BFE,
∴BE=BF,
∵BF=DF,
∴BE=ED=DF=BF,
∴四边形BEDF为菱形
【解析】(1)分别以B、D为圆心,比BD的一半长为半径画弧,交于两点,确定出垂直平分线即可;(2)连接BE,DF,四边形BEDF为菱形,理由为:由EF垂直平分BD,得到BE=DE,∠DEF=∠BEF,再由AD与BC平行,得到一对内错角相等,等量代换及等角对等边得到BE=BF,再由BF=DF,等量代换得到四条边相等,即可得证.
【考点精析】利用矩形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
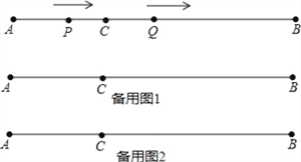
【题目】如图,AB=12cm,点C是线段AB上的一点,BC=2AC.动点P从点A出发,以3cm/s的速度向右运动,到达点B后立即返回,以3cm/s的速度向左运动;动点Q从点C出发,以1cm/s的速度向右运动.设它们同时出发,运动时间为ts.当点P与点Q第二次重合时,P、Q两点停止运动.
(1)AC=__cm,BC=__cm;
(2)当t为何值时,AP=PQ;
(3)当t为何值时,PQ=1cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国明代著名数学家程大位的《算法统宗》一书中记载了一些诗歌形式的算题,其中有一个“百羊问题”:甲赶群羊逐草茂,乙拽肥羊一只随其后;戏问甲及一百否?甲云所说无差谬,若得这般一群凑,再添半群小半群,得你一只来方凑.玄机奥妙谁猜透.题目的意思是:甲赶了一群羊在草地上往前走,乙牵了一只肥羊紧跟在甲的后面.乙问甲:“你这群羊有一百只吗?”甲说:“如果再有这么一群,再加半群,又加四分之一群,再把你的一只凑进来,才满100只.”请问甲原来赶的羊一共有多少只?如果设甲原来赶的羊一共有![]() 只,那么可列方程为______________.
只,那么可列方程为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向
以1cm/s的速度向点B运动(运动前点M与点A重合).过M,N分别作AB的垂线交直角边于P,Q两点,线段MN运动的时间为ts.
(1)若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;
(3)t为何值时,以C,P,Q为顶点的三角形与△ABC相似?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据 ![]() ≈4.6)
≈4.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com