
【题目】如图1,A,B分别在射线OA,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.如图2,若∠MON=150°,求证:△ABR为等边三角形;
(3)如图3,若△ARB∽△PEQ,求∠MON大小.

【答案】(1)证明见解析;
(2)证明见解析;
(3)∠MON=135°.
【解析】解(1)证明:∵点C、D、E分别是OA,OB,AB的中点,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四边形ODEC是平行四边形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC=![]() AO=OC=ED,CE=OD=
AO=OC=ED,CE=OD=![]() OB=DQ,
OB=DQ,
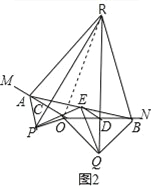
在△PCE与△EDQ中,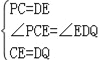 ,
,
∴△PCE≌△EDQ;
(2)如图2,连接RO,
∵PR与QR分别是OA,OB的垂直平分线,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等边三角形;
(3)由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,∵△ARB∽△PEQ,∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD=![]() ∠ARB=45°,
∠ARB=45°,
∴∠MON=135°,


科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线. 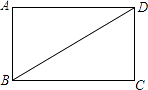
(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OE是∠AOD的平分线,OC是∠BOD的平分线.
(1)若∠AOB=130°,则∠COE是多少度?
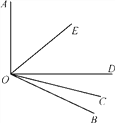
(2)在(1)的条件下,若∠COD=20°,则∠BOE是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
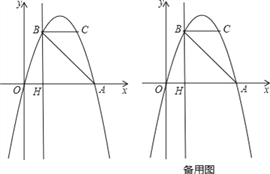
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(3)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
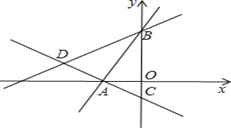
【题目】如图所示,在平面直角坐标系中,过点A(﹣![]() ,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
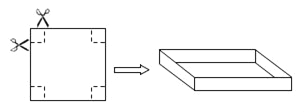
【题目】把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计)。
(1)如图,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子。
①要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由。
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2,求此时长方形盒子的长、宽、高(只需求出符合要求的一种情况)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.
(1)已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数;
(2)∠AOB=α,∠BOC=β,OM平分∠AOC,ON平分∠BOC,求∠MON的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com