【题目】如图所示，OE是∠AOD的平分线，OC是∠BOD的平分线．
(1)若∠AOB＝130°，则∠COE是多少度？
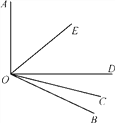
(2)在(1)的条件下，若∠COD＝20°，则∠BOE是多少度？
【答案】(1) 65°(2) 85°
【解析】试题分析：（1）直接根据角平分线的定义进行解答即可；
（2）先根据∠COD=20°求出∠BOD的度数，再根据∠AOB=130°求出∠AOD的度数，根据角平分线的定义即可得出结论．
试题解析：（1）∵OC是∠AOD的平分线，OE是∠BOD的平分线，∠AOB=130°
∴∠COE=
∠BOD+
∠AOD=
（∠BOD+∠AOD）=
∠AOB=65°；
（2）∵∠COD=20°，
∴∠BOD=2×20°=40°，
∵∠AOB=130°，
∴∠AOD=∠AOB-∠BOD=130°-40°=90°，
∵OE是∠BOD的平分线，
∴∠BOE=
∠AOD+∠BOD=
×90°+40°=85°．
科目：初中数学 来源： 题型：
【题目】△ABC中，∠C=90°，∠A=60°，AC=2cm．长为1cm的线段MN在△ABC的边AB上沿AB方向
以1cm/s的速度向点B运动（运动前点M与点A重合）．过M，N分别作AB的垂线交直角边于P，Q两点，线段MN运动的时间为ts．
（1）若△AMP的面积为y，写出y与t的函数关系式（写出自变量t的取值范围）；
（2）线段MN运动过程中，四边形MNQP有可能成为矩形吗？若有可能，求出此时t的值；若不可能，说明理由；
（3）t为何值时，以C，P，Q为顶点的三角形与△ABC相似？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红同学要测量A、C两地的距离，但A、C之间有一水池，不能直接测量，于是她在A、C同一水平面上选取了一点B，点B可直接到达A、C两地．她测量得到AB=80米，BC=20米，∠ABC=120°．请你帮助小红同学求出A、C两点之间的距离．（参考数据 
≈4.6）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点O是正方形ABCD两对角线的交点，分别延长OD到点G，OC到点E，使OG=2OD，OE=2OC，然后以OG、OE为邻边作正方形OEFG，连接AG，DE．
(1)、求证：DE⊥AG；
(2)、如图2，正方形ABCD固定，将正方形OEFG绕点O逆时针旋转α角（0°＜α＜360°），得到正方形OE′F′G′；
①在旋转过程中，当∠OAG′是直角时，求α的度数；
②若正方形ABCD的边长为2，在旋转过程中，求AF′长的最大值和此时α的度数，直接写出结果不必说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学习了有理数的乘法后，老师给同学们布置这样一道题目：计算49
×（–5），看谁算的又快又对，有三位同学的解法如下：
小军：原式 =（49 + 
）×（–5）= 49×（–5）+ 
×（–5）
=–245–4
=–249
；
小明：原式 = –
× 5 = –
= – 249 
；
小丽：原式 =（49 + 
）×（-5）=（50 -1 + 
）×（-5）
=（50 - 
）×（-5）= 50 ×（-5）+（ - 
） ×（-5）
= –250 +
= –249
；
（1）对于以上三种解法，你认为谁的解法较好？
（2）上面的解法对你有何启发，用你认为最合适的方法计算：
19
×（– 8）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小红同学要测量A、C两地的距离，但A、C之间有一水池，不能直接测量，于是她在A、C同一水平面上选取了一点B，点B可直接到达A、C两地．她测量得到AB=80米，BC=20米，∠ABC=120°．请你帮助小红同学求出A、C两点之间的距离．（参考数据 
≈4.6） 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，A，B分别在射线OA，ON上，且∠MON为钝角，现以线段OA，OB为斜边向∠MON的外侧作等腰直角三角形，分别是△OAP，△OBQ，点C，D，E分别是OA，OB，AB的中点．
（1）求证：△PCE≌△EDQ；
（2）延长PC，QD交于点R．如图2，若∠MON=150°，求证：△ABR为等边三角形；
（3）如图3，若△ARB∽△PEQ，求∠MON大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列算式：12-02=1+0=1，,22-12=2+1=3,32-22=3+2=5,42-32=4+3=7 ，52-42=5+4=9，…….
若字母 
表示自然数，请把你观察到的规律用含有 
的式子表示出来________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com