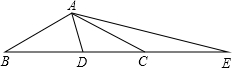
解:(1)因为AB=AC,
所以∠B=∠ACB=30°,
因为BA=BD,所以,∠BAD=∠BDA=75°,
所以∠DAC=45°,
又有CA=CE,
所以∠E=∠CAE=15°,
所以∠DAE=∠DAC+∠CAE=60°;
(2)不改变;令∠B=x°,BA=BD,
所以∠BAD=∠BDA=
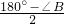
=90°-

x°,
∠ACB=180°-∠ACE=∠B+∠BAC,得∠ACB=60°-x°,
所以∠DAC=∠ADB-∠ACD=30°+

x°,
又因为CA=CE,
所以∠E=∠CAE=30°-

x°,
所以∠DAE=∠DAC+∠CAE=60°
(3)

α°.
设∠B=x°,
∵BA=BD,
所以∠BAD=∠BDA=90°-

x°,∠ACB=180°-x°-α°,
所以∠DAC=∠ADB-∠ACD=-90°+

x°+α°,
又因为CA=CE,
所以∠E=∠CAE=90°-

x°-

α°,
所以∠DAE=∠DAC+∠CAE=

α°
分析:(1)要求∠DAE的度数,只要求出∠DAC+∠CAE的度数.∠DAC=∠BAC-∠BAD.只要求出∠BAD的度数,∠BAD=

(180°-∠B),而∠B=

(180°-∠BAC),而∠CAE的度数,∵CE=CA∴∠E=∠CAE,利用三角形外角性质得,∠CAE=

∠ACB;而∠ACB=

(180°-∠BAC);
(2)设∠B=x°,等腰三角形的性质得,∠BAD=∠BDA=90°-

x°,三角形的内角和定理得,∠ACB=60°-x,所以,∠DAC=∠ADB-∠ACD=30°+

x°,由等腰三角形的性质得∠E=∠CAE=30°-

x°,所以∠DAE=∠DAC+∠CAE=60°
(3)设∠B=x°,等腰三角形的性质得,∠BAD=∠BDA=90°-

x°,三角形的内角和定理得,∠ACB=180°-x°-α°,所以,∠DAC=∠ADB-∠ACD=-90°+

x°+α°,由等腰三角形的性质得∠E=∠CAE=90°-

x°-

α°,所以∠DAE=∠DAC+∠CAE=

α°
点评:考查等腰三角形的性质,内角和定理,外角性质等知识.多次利用外角的性质得到角之间的关系式正确解答本题的关键.

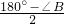 =90°-
=90°- x°,
x°, x°,
x°, x°,
x°, α°.
α°. x°,∠ACB=180°-x°-α°,
x°,∠ACB=180°-x°-α°, x°+α°,
x°+α°, x°-
x°- α°,
α°, α°
α° (180°-∠B),而∠B=
(180°-∠B),而∠B= (180°-∠BAC),而∠CAE的度数,∵CE=CA∴∠E=∠CAE,利用三角形外角性质得,∠CAE=
(180°-∠BAC),而∠CAE的度数,∵CE=CA∴∠E=∠CAE,利用三角形外角性质得,∠CAE= ∠ACB;而∠ACB=
∠ACB;而∠ACB= (180°-∠BAC);
(180°-∠BAC); x°,三角形的内角和定理得,∠ACB=60°-x,所以,∠DAC=∠ADB-∠ACD=30°+
x°,三角形的内角和定理得,∠ACB=60°-x,所以,∠DAC=∠ADB-∠ACD=30°+ x°,由等腰三角形的性质得∠E=∠CAE=30°-
x°,由等腰三角形的性质得∠E=∠CAE=30°- x°,所以∠DAE=∠DAC+∠CAE=60°
x°,所以∠DAE=∠DAC+∠CAE=60° x°,三角形的内角和定理得,∠ACB=180°-x°-α°,所以,∠DAC=∠ADB-∠ACD=-90°+
x°,三角形的内角和定理得,∠ACB=180°-x°-α°,所以,∠DAC=∠ADB-∠ACD=-90°+ x°+α°,由等腰三角形的性质得∠E=∠CAE=90°-
x°+α°,由等腰三角形的性质得∠E=∠CAE=90°- x°-
x°- α°,所以∠DAE=∠DAC+∠CAE=
α°,所以∠DAE=∠DAC+∠CAE= α°
α°

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为