
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在-起,连接AC、BD。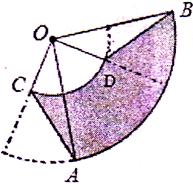
(1)AC与BD相等吗?为什么?
(2)若0A=2cm,OC=lcm,求图中阴影部分的面积。
科目:初中数学 来源: 题型:单选题
⊙O的半径为5cm,点A、B、C是直线a上的三点,OA、OB、OC的长度分别是5cm、4cm、7cm,则直线a与⊙O的位置关系是: ( )
A.相离 B.相切 C.相交 D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
维修人员为更换一圆柱形的输水管道,需先确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面,若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=DB,∠B=30°,若⊙O的半径为4.
(1)求证:BD是⊙O的切线;
(2)求CB的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:解答题
(本题满分13分)如图1,反比例函数 (
( )的图象经过点A(
)的图象经过点A( ,1),射线AB与反比例函数图象交与另一点B(1,
,1),射线AB与反比例函数图象交与另一点B(1, ),射线AC与
),射线AC与 轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.


(1)求 的值;
的值;
(2)求∠DAC的度数及直线AC的解析式;
(3)如图2,M是线段AC上方反比例函数图象上一动点,过M作直线 轴,与AC相交于N,连接CM,求△CMN面积的最大值.
轴,与AC相交于N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:解答题
(本题满分8分)已知: ,
, 与
与 成正比例,
成正比例, 与x成反比例,且
与x成反比例,且 时,
时, ;
; 时,
时, .求
.求 时,y的值.
时,y的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA、OB在点O钉在一起,并使它们保持垂直,在测直径时,把点O靠在圆周上,读得刻度OE=6个单位,OF=8个单位,则圆的直径为( )

A.8个单位 B.10个单位 C.12个单位 D.15个单位
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省伊春市九年级11月月考数学试卷(解析版) 题型:选择题
小明想用扇形纸片围成一个圆锥,已知扇形的半径为5 cm,弧长是 cm,那么围成的圆锥的高度是( )
cm,那么围成的圆锥的高度是( )
A.5 cm B.4 cm C.3 cm D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com