Question

13．如图1，是全国最大的瓷碗造型建筑坐落于江西景德镇，整体造型概念来自“宋代影青斗笠碗”，造型庄重典雅，象征“万瓷之母”．小敏为了计算该建筑物的横断面（瓷碗横断面ABCD为等腰梯形）的高度如图2，她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°，而后沿着一段坡度为0.44的小坡PQ步
行到点Q（此过程中AD、AP、PQ始终处于同一平面）后测得点D的仰角减少了5°．已知坡PQ的水平距离为20米，小敏身高忽略不计．
（1）试计算该瓷碗建筑物的高度？
（2）小敏测得AD与水平面夹角约为58°，底座直径AB约为20米，试计算碗口CD的直径为多少米？
坡度：坡与水平线夹角的正切值．参考数据：sin40°≈0.64，tan40°≈0.84，sin58°≈0.85，tan58°≈1.60．

Answer 1

分析 （1）根据∠DPA=45°得到DH=PH，根据正切的定义求出PM，求出a；
（2）根据正切的定义计算即可．

解答 解：（1）分别过点D与点P向水平线引垂线与过点Q的水平线交于点N与点M，与PA交于点H，
∵∠DPA=45°，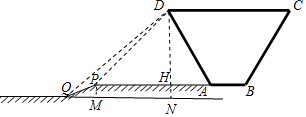
∴DH=PH，
设为a，
∵tan∠PQM=$\frac{PM}{QM}$=0.44，QM=20，
∴PM=0.44×QM=8.8．
tan∠DQN=$\frac{DN}{QN}$=0.84，即$\frac{a+8.8}{a+20}=0.84$，
解得：a=50．
答：该瓷碗建筑物的高度为50米．
（2）∵DH=50，且$tan∠DAH=\frac{DH}{AH}=1.6$，
∴AH=31.25．
∴CD=AB+2AH=82.5．
答：该瓷碗建筑物碗口CD的直径为82.5米．

点评 本题考查的是解直角三角形的应用，掌握仰角俯角的概念、坡度坡角的概念、熟记锐角三角函数的定义是解题的关键．