
如图,有长为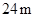 的篱笆,现一面利用墙(墙的最大可用长度
的篱笆,现一面利用墙(墙的最大可用长度 为
为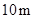 )围成中间隔有一道篱笆的长方形花圃,设花圃的宽
)围成中间隔有一道篱笆的长方形花圃,设花圃的宽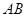 为
为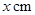 ,面积为
,面积为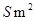 .
.
(1)求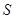 与
与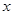 的函数关系式.
的函数关系式.
(2)要围成面积为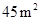 的花圃,
的花圃,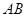 的长是多少米?
的长是多少米?
(3)能围成面积比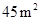 还大的花圃吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.
还大的花圃吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.

(1)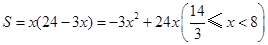 ;(2)
;(2)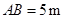 ;
;
(3)长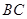 为
为 ,宽为
,宽为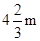 .这时花圃面积最大,为
.这时花圃面积最大,为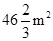 .
.
【解析】
试题分析:(1)现年表示出BC的长,再根据矩形面积公式即得函数关系式;
(2)把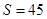 代入(1)中的函数关系式,即可求得结果,注意对所求值的取舍;
代入(1)中的函数关系式,即可求得结果,注意对所求值的取舍;
(3)求出(1)中的函数的最大值即可。
(1)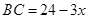 ,故
,故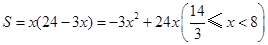 .
.
(2)由已知得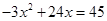 ,即
,即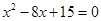 ,解得
,解得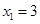 ,
,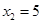 ,
,
当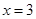 时,
时,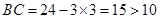 ,不合题意,故
,不合题意,故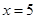 ,即
,即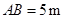 .
.
(3)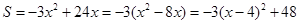 .
.
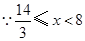 ,
,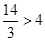 ,
,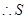 随着
随着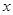 的增大而减小.
的增大而减小.
故当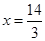 时,
时,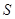 有最大值
有最大值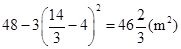 .
.
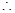 能围成面积比
能围成面积比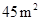 还大的花圃.
还大的花圃.
围法: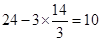 ,花圃的长
,花圃的长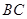 为
为 ,宽为
,宽为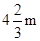 .这时花圃面积最大,为
.这时花圃面积最大,为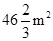 .
.
考点:本题考查的是二次函数的应用
点评:解答本题的关键是运用长方形面积计算方法列一元二次方程解决实际问题与根的判别式的应用.


科目:初中数学 来源: 题型:
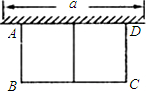 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:查看答案和解析>>
科目:初中数学 来源: 题型:
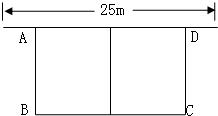 24、如图,有长为48米的篱笆,一面利用墙(墙的最大可用长度25米),围成中间隔有一道篱笆的长方形花圃ABCD.
24、如图,有长为48米的篱笆,一面利用墙(墙的最大可用长度25米),围成中间隔有一道篱笆的长方形花圃ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有长为24的篱笆,围成矩形花圃,且花圃的长可借用一段墙体(墙体的最大可用长度是10米),求围成的花圃面积y与AB的长x的函数关系,并确定y的最大值.
如图,有长为24的篱笆,围成矩形花圃,且花圃的长可借用一段墙体(墙体的最大可用长度是10米),求围成的花圃面积y与AB的长x的函数关系,并确定y的最大值.查看答案和解析>>
科目:初中数学 来源: 题型:
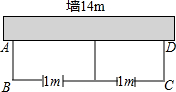 如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门,此时花圃的面积刚好为45米2,求此时花圃的长和宽.
如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门,此时花圃的面积刚好为45米2,求此时花圃的长和宽.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com