
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
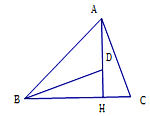
(1)求证:![]()
(2)如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别对应点
分别对应点![]() ),设射线
),设射线![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间满足的数量关系,并说明理由.
之间满足的数量关系,并说明理由.
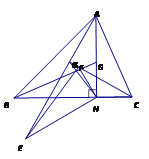
【答案】(1)证明见解析(2)EF=2HG
【解析】分析:(1)先判断出AH=BH,再判断出△BHD≌△AHC即可求解.(2)方法一、先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可;方法二、取EF的中点K,连接GK,HK,先证明GK=HK=
,然后判断出△AQC∽△GQH,用相似比即可;方法二、取EF的中点K,连接GK,HK,先证明GK=HK=![]() EF,再证明△GKH是等边三角形即可.
EF,再证明△GKH是等边三角形即可.
详解:(1)在Rt△AHB中,∠ABC=45°,
∴AH=BH,
在△BHD和△AHC中,
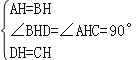 ,
,
∴△BHD≌△AHC,
∴![]()
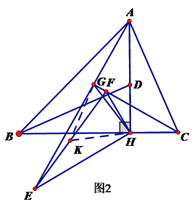
(2)方法1:如图1,
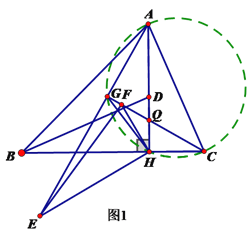
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQH,
∴△AQC∽△GQH,
∴![]() ,
,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴EF=BD,
由(1)知,BD=AC,
∴EF=AC
∴![]()
即:EF=2HG.
方法2:如图2,取EF的中点K,连接GK,HK,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
由旋转知,∠EHF=90°,
∴EK=HK=![]() EF
EF
∴EK=GK=![]() EF,
EF,
∴HK=GK,
∵EK=HK,
∴∠FKG=2∠AEF,
∵EK=GK,
∴∠HKF=2∠HEF,
由旋转知,∠AHF=30°,
∴∠AHE=120°,
由(1)知,BH=AH,
∵BH=EH,
∴AH=EH,
∴∠AEH=30°,
∴∠HKG=∠FKG+∠HKF=2∠AEF+2∠HEF=2∠AEH=60°,
∴△HKG是等边三角形,
∴GH=GK,
∴EF=2GK=2GH,
即:EF=2GH.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
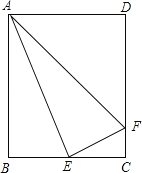
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
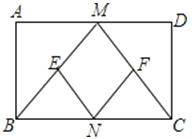
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:在数轴上,点M表示实数为x,点N表示实数为y,当x<y 时,点M,N之间的距离记作:MN =Y-X;当x>y时,点M,N之间的距离记作:MN = x-y,例如:x=-3,y=2, 则MN =2-(-3)=5.
如图,点A,B,C是数轴上从左向右依次排列的三点,且AC=17,BC=11,点B表示的数是-6.
![]()
(1) 点A表示的数是 ,点C表示的数是 ;
(2) 动点M,N分别从A,C同时出发,点M沿数轴向右运动,速度为1个单位长度∕秒,点N沿数轴向左运动,速度为2个单位长度∕秒,运动t秒后:
①点M表示的数 ,点N表示的数 ;(用含t的代数式表示)
②求当t为何值时,点M,N,B三点中相邻两个点之间的距离相等.(M、N、B三点中任意两点不重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知PA=PB=PC=2,∠BPC=120°,PA∥BC.以AB、PB为边作平行四边形ABPD,连接CD,则CD的长为( )

A. 2![]() B. 2
B. 2![]() C.
C. ![]() +1D.
+1D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=![]() ,反比例函数y=
,反比例函数y=![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推广“阳光体育”大课间活动,高新中学对已开设的A实心球,B立定跳远,C跑步,D排球四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
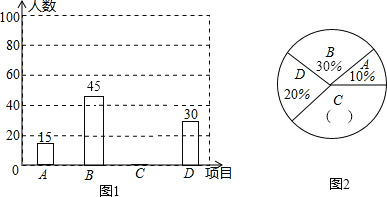
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了3名喜欢“跑步”的学生,其中有2名男生,1名女生,现从这3名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC=4,将△ABC翻折,使得点A落在BC的中点A'处,折痕分别交边AB、AC于点D、点E,那么AD:AE的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com