
【题目】如图,在平面直角坐标系![]() 中,已知二次函数图象与
中,已知二次函数图象与![]() 正半轴交于点
正半轴交于点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() .若过点
.若过点![]() 作平行于
作平行于![]() 轴的直线交抛物线于点
轴的直线交抛物线于点![]() .
.
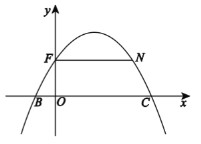
(1)点![]() 的横坐标为______;
的横坐标为______;
(2)设抛物线的顶点为点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,该二次函数有最大值3,试求
时,该二次函数有最大值3,试求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
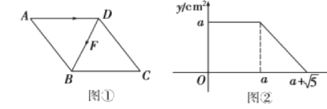
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,用树状图表示或列表法求足球踢到了小华处的概率是多少
(2)如果从小明开始踢,经过踢三次后,球踢到了小明处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
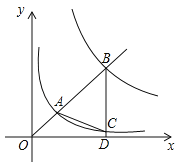
【题目】(2017浙江省湖州市,第16题,4分)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数![]() 和
和![]() 在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交
在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交![]() 的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
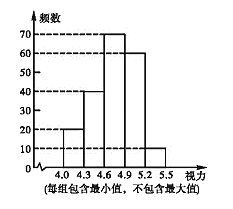
【题目】建华区对参加![]() 年中考的
年中考的![]() 名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图、表信息解答下列问题:
名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图、表信息解答下列问题:
(1)在频数分布表中,![]() 的值为 ,
的值为 ,![]() 的值为 ,并将频数分布直方图补充完整;
的值为 ,并将频数分布直方图补充完整;
(2)甲同学说:“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围?
(3)若视力在![]() 以上(含
以上(含![]() )均属正常,则视力正常的人数占被统计人数的百分比是 ,并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
)均属正常,则视力正常的人数占被统计人数的百分比是 ,并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
视力 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“守护碧水蓝天,守护我们的家园”,某市为了改善城市环境,预算 116 万元购进 A、B 两种型号的清扫机,已知 A 型号清扫机的单价比 B 型号清扫 机单价的 ![]() 多 1.2 万元,若购进 2 台 A 型号清扫机和 3 台 B 型号清扫机花费 54.6 万元.
多 1.2 万元,若购进 2 台 A 型号清扫机和 3 台 B 型号清扫机花费 54.6 万元.
(1)求 A 型号清扫机和 B 型号清扫机的单价分别为多少万元;
(2)该市通过考察决定先购进两种型号的清扫机共 10 台,且 B 型号的清扫机 数量不能少于 A 型号清扫机的 1.5 倍,该市怎样购买才能花费最少?最少花费 多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
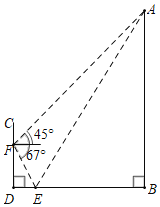
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上(如图所示).该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为45°,平面镜E的俯角为67°,测得FD=2.4米.求旗杆AB的高度约为多少米?(结果保留整数,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com