分析:过A作AC垂直于x轴,过B作BD垂直于x轴,由A在反比例函数y=
上,B在反比例函数y=
上,利用反比例函数k的几何意义求出三角形AOC与三角形BOD的面积,再由OA与OB垂直得到一对角互余,由AC垂直于x轴得到直角三角形AOC中两锐角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,利用两对对应角相等的两三角形相似,得到三角形BOD与三角形AOC相似,由面积之比等于相似比的平方,由面积比求出相似比,在直角三角形AOB中,利用锐角三角函数定义即可求出tan∠OAB的值.
解答: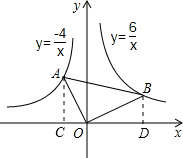
解:过A作AC⊥x轴,过B作BD⊥轴,
∵A在反比例函数y=
上,B在反比例函数y=
上,
∴S
△AOC=
×|-4|=2,S
△BOD=
×6=3,
∵AC⊥CO,OA⊥OB,BD⊥OD
∴∠CAO+∠COA=90°,∠COA+∠BOD=90°,∠ACO=∠ODB=90°,
∴∠CAO=∠BOD,
∴△BDO∽△OCA,
又∵S
△BDO:S
△OCA=3:2,
∴BO:OA=
:
,
在Rt△AOB中,tan∠OAB=
=
=
.
故答案为:
.
点评:此题属于反比例函数综合题,涉及的知识有:相似三角形的判定与性质,反比例函数中k的几何意义,以及锐角三角函数定义,作出相应的辅助线是解本题的关键.

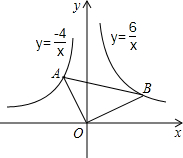 如图,Rt△ABC中,∠AOB=90°,点A在y=-
如图,Rt△ABC中,∠AOB=90°,点A在y=- 解:过A作AC⊥x轴,过B作BD⊥轴,
解:过A作AC⊥x轴,过B作BD⊥轴,


 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.