
【题目】如图,反映的是小丽从家外出到最终回家,离家距离![]() (米)与时间
(米)与时间![]() (分)的关系图。请根据图像回答下列问题:
(分)的关系图。请根据图像回答下列问题:
(1)小丽在A点表示含义:出发后______分钟时,离家距离______米;
(2)出发后6-10分钟之间可能发生了什么情况:______________________________,出发后14-18分钟之间可能发生了什么情况: ________________________.
(3)在28分钟内的行进过程中,____________段时间的速度最慢,为____________米分;
(4)小丽在回家路上,第28分钟时停了4分钟,之后立即以100米/分的速度回到家.请写出计算过程,并在图中补上28分钟以后的路程![]() 与时间
与时间![]() 关系图。
关系图。
(5)小丽一开始从家外出到最终回家,中途共停留了____________分钟.

【答案】(1)2,150;(2)忘记带东西;中途休息;(3)6-10段,37.5分/米;(4)见解析;
(5)18分钟.
【解析】
(1)根据函数图像即可得到A点的含义;(2)根据6-10分钟离家的距离减小到0即可求解,14-18分钟之间距离不变即可求解;(3)根据函数图像的倾斜角度即可判断速度的快慢,再根据函数图像求出此阶段的速度;(4)求出到家所需的时间,即可进行补全;
(5)把距离不变的时间相加即可求解.
(1)(1)小丽在A点表示含义:出发后2分钟时,离家距离150米;
(2)出发后6-10分钟之间可能发生了什么情况:忘记带东西,出发后14-18分钟之间可能发生了什么情况:在家休息.
(3)在28分钟内的行进过程中,6-10段时间的速度最慢,为37.5米/分;
(4)到家所需的时间为![]() 分钟,
分钟,
故补全函数如下:
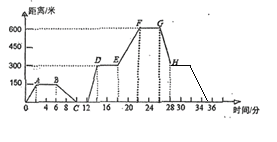
(5)小丽一开始从家外出到最终回家,中途共停留了4+2+4+4+4=18分钟.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 为
为![]() 上一动点,作
上一动点,作![]() 平行
平行![]() ,交
,交![]() 于F,在
于F,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)根据题意补全图形;
(2)求证四边形![]() 是平行四边形;
是平行四边形;
(3)若![]() ,写出一个
,写出一个![]() 的度数,使得四边形
的度数,使得四边形![]() 是菱形.
是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,过
边上的中线,过![]() 作
作![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,则下列结论正确的是______.(请填写序号)
,则下列结论正确的是______.(请填写序号)
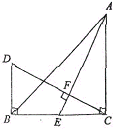
①若![]() ,则
,则![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥连接
;⑥连接![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
【答案】(1)A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元;(2)最少购进A品牌工具套装17套.
【解析】试题分析:(1)利用两种套装的套数作为等量关系列方程求解.(2)利用总获利大于等于120,解不等式.
试题解析:
(1)解:设B种品牌套装每套进价为x元,则A种品牌套装每套进价为(x+2.5)元.
根据题意得: ![]() =2×
=2×![]() ,
,
解得:x=7.5,
经检验,x=7.5为分式方程的解,
∴x+2.5=10.
答:A种品牌套装每套进价为10元,B种品牌套装每套进价为7.5元.
(2)解:设购进A品牌工具套装a套,则购进B品牌工具套装(2a+4)套,
根据题意得:(13﹣10)a+(9.5﹣7.5)(2a+4)>120,
解得:a>16,
∵a为正整数,
∴a取最小值17.
答:最少购进A品牌工具套装17套.
点睛:分式方程应用题:一设,一般题里有两个有关联的未知量,先设出一个未知量,并找出两个未知量的联系;二列,找等量关系,列方程,这个时候应该注意的是和差分倍关系:三解,正确解分式方程;四验,应用题要双检验;五答,应用题要写答.
【题型】解答题
【结束】
26
【题目】四边形ABCD内接于⊙O,点E为AD上一点,连接AC,CB,∠B=∠AEC.
(1)如图1,求证:CE=CD;

(2)如图2,若∠B+∠CAE=120°,∠ACD=2∠BAC,求∠BAD的度数;

(3)如图3,在(2)的条件下,延长CE交⊙O于点G,若tan∠BAC= ![]() ,EG=2,求AE的长.
,EG=2,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,△ABC是等边三角形,点D是边BC上任意一点(不与B、C重合),点E在边AC上,∠ADE=60°,∠BAD与∠CDE有怎样的数量关系,并给予证明.
(2)如图②,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合), ∠ADE=∠B,点E在边AC上.若CE=BD=3,BC=8,求AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )

A.4B.5C.6D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com