
【题目】(1)如图①,△ABC是等边三角形,点D是边BC上任意一点(不与B、C重合),点E在边AC上,∠ADE=60°,∠BAD与∠CDE有怎样的数量关系,并给予证明.
(2)如图②,在△ABC中,AB=AC,点D是边BC上一点(不与B、C重合), ∠ADE=∠B,点E在边AC上.若CE=BD=3,BC=8,求AB的长度.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图:小刚站在河边的![]() 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的![]() 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树![]() 处,接着再向前走了30步到达
处,接着再向前走了30步到达![]() 处,然后他左转
处,然后他左转![]() 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置![]() 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.
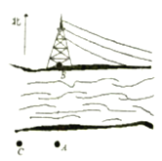
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点![]() 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反映的是小丽从家外出到最终回家,离家距离![]() (米)与时间
(米)与时间![]() (分)的关系图。请根据图像回答下列问题:
(分)的关系图。请根据图像回答下列问题:
(1)小丽在A点表示含义:出发后______分钟时,离家距离______米;
(2)出发后6-10分钟之间可能发生了什么情况:______________________________,出发后14-18分钟之间可能发生了什么情况: ________________________.
(3)在28分钟内的行进过程中,____________段时间的速度最慢,为____________米分;
(4)小丽在回家路上,第28分钟时停了4分钟,之后立即以100米/分的速度回到家.请写出计算过程,并在图中补上28分钟以后的路程![]() 与时间
与时间![]() 关系图。
关系图。
(5)小丽一开始从家外出到最终回家,中途共停留了____________分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEB都是等边三角形,点A、D、B在同一直线上,如图1.
(1)求证:DC=AE;
(2)若BM⊥CD,BN⊥AE,垂足分别为M、N,如图2,求证:△BMN是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
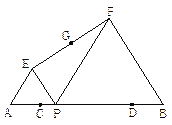
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
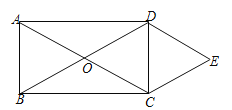
(1)求证:四边形OCED是菱形;
(2)若AB=3,AD=4,求四边形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .过点
.过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .若
.若![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②点
;②点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确结论的序号是( )
;其中正确结论的序号是( )

A.①③④B.①②⑤C.③④⑤D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
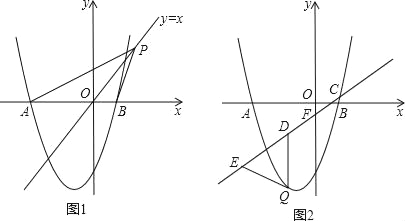
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=![]() x﹣
x﹣![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com