
【题目】已知A,B两地相距120km,甲,乙两人分别从两地出发相向而行,甲先出发,中途加油休息一段时间,然后以原来的速度继续前进,两人离A地的距离y(km)与甲出发时间x(h)的关系式如图所示,请结合图象解答下列问题:
(1)甲行驶过程中的速度是多少km/h,途中休息的时间为多少h.
(2)求甲加油后y与x的函数关系式,并写出自变量x的取值范围;
(3)甲出发多少小时两人恰好相距10km?
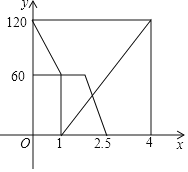
【答案】(1)甲的速度为60 km/h;休息了0.5h;(2)y=﹣60x+150(1.5≤x≤2.5);(3)甲出发1.8小时或2小时两车相距10km.
【解析】
(1)由图象可知,甲在前1小时走了60千米,计算速度即可;由于甲的速度未改变,故走完全程不休息需要2小时,而图象可知用了2.5小时,相减即可求出休息时间;
(2)设甲加油后y=kx+b,将图象上两点(1.5,60)和(2.5,0)代入即可求出解析式;
(3)先算出乙路程y1和x的关系式,再根据|y-y1|=10列出方程计算即可.
解:(1)根据甲的图象可知前1小时走了120﹣60千米,故甲的速度为60 km/h;
甲走120千米需要2小时,而他到达终点的时间是2.5小时,故休息了0.5h.
故答案为:60;0.5.
(2)设甲加油后y=kx+b,将(1.5,60)和(2.5,0)代入解析式,
![]() ,解得
,解得![]() .
.
故y=﹣60x+150(1.5≤x≤2.5).
(3)设乙路程y1=k1x+![]() ,将(1,0)和(4,120)代入
,将(1,0)和(4,120)代入
![]() ,解得
,解得![]() .
.
故y1=40x﹣40.
当x=1.5时,y1=40×1.5﹣40=20,此时两车相距60﹣20=40千米.
故相距10km时间段为1.5h~2.5小时之间.
依题意得,|(﹣60x+150)﹣(40x﹣40)|=10
解得,x=1.8或2
故甲出发1.8小时或2小时两车相距10km.
故答案为:(1)甲的速度为60 km/h;休息了0.5h;(2)y=﹣60x+150(1.5≤x≤2.5);(3)甲出发1.8小时或2小时两车相距10km.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,D是AC的中点,CE⊥BD于点E,交BA的延长线于点F.若BF=12,则△FBC的面积为( )

A. 40 B. 46 C. 48 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值;
的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
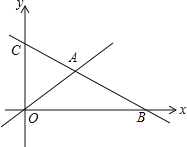
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴,y轴交于点B,C且与直线y=
x+6分别与x轴,y轴交于点B,C且与直线y=![]() x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
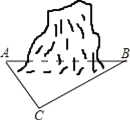
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
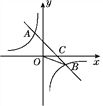
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限的A,B两点,与x轴交于C点.已知A(-2,m),B(n,-2),tan ∠BOC=
(k≠0)的图象交于第二、四象限的A,B两点,与x轴交于C点.已知A(-2,m),B(n,-2),tan ∠BOC=![]() ,则此一次函数的解析式为________________.
,则此一次函数的解析式为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场普通门票价格40元/张,为了促销,新推出两种办卡方式:
①白金卡售价200元/张,每次凭卡另收取20元;
②钻石卡售价1000元/张,每次凭卡不再收费.
促销期间普通门票正常出售,两种优惠卡不限次数,设去游乐场玩x次时,所需总费用为y元.
(1)分别写出选择白金卡、普通门票消费时,y与x之间的函数关系式.
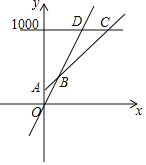
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B,C的坐标.
(3)请根据图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com