
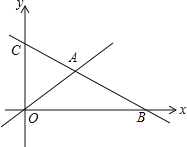
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴,y轴交于点B,C且与直线y=
x+6分别与x轴,y轴交于点B,C且与直线y=![]() x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
【答案】(![]() ,
,![]() )或(﹣4,﹣2).
)或(﹣4,﹣2).
【解析】
解方程或方程组得到A(6,3),B(12,0),C(0,6),①当∠ADC=90°,得到CD⊥OA,设直线CD的解析式为:y=-2x+b,求得直线CD的解析式为:y=-2x+6,解方程组得到D(![]() ,
,![]() ),②当∠ACD=90°,得到DC⊥BC,设直线CD的解析式为:y=2x+a,把C(0,6)代入得,a=6,求得直线CD的解析式为:y=2x+6,解方程组得到D(-4,-2).
),②当∠ACD=90°,得到DC⊥BC,设直线CD的解析式为:y=2x+a,把C(0,6)代入得,a=6,求得直线CD的解析式为:y=2x+6,解方程组得到D(-4,-2).
解:(1)直线y=﹣![]() x+6,
x+6,
当x=0时,y=6,
当y=0时,x=12,
则B(12,0),C(0,6),
解方程组: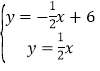 得:
得:![]() ,
,
则A(6,3),
故A(6,3),B(12,0),C(0,6),
∵△ACD为直角三角形,
∴①当∠ADC=90°,
∴CD⊥OA,
∴设直线CD的解析式为:y=﹣2x+b,
把C(0,6)代入得,b=6,
∴直线CD的解析式为:y=﹣2x+6,
解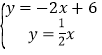 得
得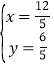 ,
,
∴D(![]() ,
,![]() ),
),
②当∠ACD=90°,
∴DC⊥BC,
∴设直线CD的解析式为:y=2x+a,
把C(0,6)代入得,a=6,
∴直线CD的解析式为:y=2x+6,
解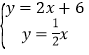 得,
得,![]() ,
,
∴D(﹣4,﹣2),
综上所述:点D的坐标为(![]() ,
,![]() )或(﹣4,﹣2).
)或(﹣4,﹣2).
故答案为:(![]() ,
,![]() )或(﹣4,﹣2).
)或(﹣4,﹣2).


科目:初中数学 来源: 题型:
【题目】把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕A点旋转时,两边分别交直线BC,CD于点M、N.
(1)如图①,当M、N分别在边BC,CD上时,作AE垂直于AN,交CB的延长线于点E,求证:△ABE≌△ADN;
(2)如图②,当M、N分别在边CB,DC的延长线上时,求证:MN+BM=DN;
(3)如图③,当M、N分别在边CB,DC的延长线上时,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
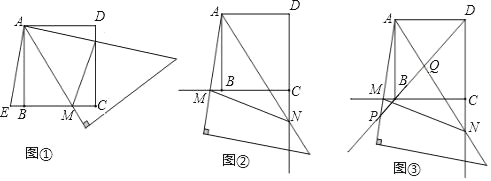
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
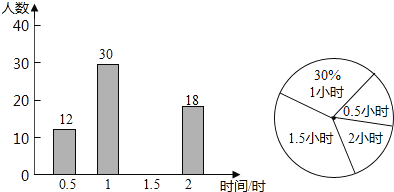
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从E点射出一束光线经OA上一点D反射,此时∠ODE=∠ADC,且反射光线DC恰好与OB平行,则∠DEB的度数是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
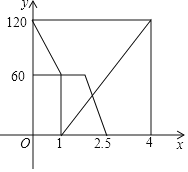
【题目】已知A,B两地相距120km,甲,乙两人分别从两地出发相向而行,甲先出发,中途加油休息一段时间,然后以原来的速度继续前进,两人离A地的距离y(km)与甲出发时间x(h)的关系式如图所示,请结合图象解答下列问题:
(1)甲行驶过程中的速度是多少km/h,途中休息的时间为多少h.
(2)求甲加油后y与x的函数关系式,并写出自变量x的取值范围;
(3)甲出发多少小时两人恰好相距10km?
查看答案和解析>>
科目:初中数学 来源: 题型:
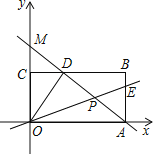
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com