
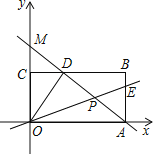
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
【答案】(1)点D的坐标为(2,6).直线OP的解析式为y=![]() x.(2)点N的坐标为(3,5)或(13,-5).(3)在线段AE上存在一点Q,使得△FGQ为等腰直角三角形,当t=
x.(2)点N的坐标为(3,5)或(13,-5).(3)在线段AE上存在一点Q,使得△FGQ为等腰直角三角形,当t=![]() 时点Q的坐标为(8,
时点Q的坐标为(8,![]() )或(8,
)或(8,![]() ),当t=
),当t=![]() 时点Q的坐标为(8,
时点Q的坐标为(8,![]() ).
).
【解析】
(1)根据长方形的性质可得出点A的坐标,利用待定系数法可求出直线AD的解析式,利用一次函数图象上点的坐标特征可求出点D的坐标,再由点P是AD的中点可得出点P的坐标,进而可得出正比例函数OP的解析式;
(2)利用三角形面积的公式可求出S△ODP的值,由直线OP的解析式,利用一次函数图象上点的坐标特征可得出点E的坐标,设点N的坐标为(m,-m+8),由△AEN的面积等于△ODP的面积,可得出关于m的含绝对值符号的一元一次方程,解之即可得出m的值,再将其代入点N的坐标中即可得出结论;
(3)由点T的坐标可得出点F,G的坐标,分∠FGQ=90°、∠GFQ=90°及∠FQG=90°三种情况考虑:①当∠FGQ=90°时,根据等腰直角三角形两直角边相等可得出关于t的一元一次方程,解之可得出t值,再利用等腰直角三角形的性质可得出点Q的坐标;②当∠GFQ=90°时,根据等腰直角三角形两直角边相等可得出关于t的一元一次方程,解之可得出t值,再利用等腰直角三角形的性质可得出点Q的坐标;③当∠FQG=90°时,过点Q作QS⊥FG于点S,根据等腰直角三角形斜边等于斜边上高的二倍可得出关于t的一元一次方程,解之可得出t值,再利用等腰直角三角形的性质可得出点Q的坐标.综上,此题得解.
(1)∵四边形OABC为长方形,点B的坐标为(8,6),
∴点A的坐标为(8,0),BC∥x轴.
∵直线y=-x+b经过点A,
∴0=-8+b,
∴b=8,
∴直线AD的解析式为y=-x+8.
当y=6时,有-x+8=6,
解得:x=2,
∴点D的坐标为(2,6).
∵点P是AD的中点,
∴点P的坐标为(![]() ,
,![]() ),即(5,3),
),即(5,3),
∴直线OP的解析式为y=![]() x.
x.
(2)S△ODP=S△ODA-S△OPA,
=![]() ×8×6-
×8×6-![]() ×8×3,
×8×3,
=12.
当x=8时,y=![]() x=
x=![]() ,
,
∴点E的坐标为(8,![]() ).
).
设点N的坐标为(m,-m+8).
∵S△AEN=S△ODP,
∴![]() ×
×![]() ×|8-m|=12,
×|8-m|=12,
解得:m=3或m=13,
∴点N的坐标为(3,5)或(13,-5).
(3)∵点T的坐标为(t,0)(5<t<8),
∴点F的坐标为(t,![]() t),点G的坐标为(t,-t+8).
t),点G的坐标为(t,-t+8).
分三种情况考虑:
①当∠FGQ=90°时,如图1所示.
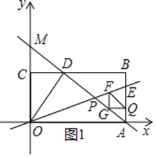
∵△FGQ为等腰直角三角形,
∴FG=GQ,即![]() t-(-t+8)=8-t,
t-(-t+8)=8-t,
解得:t=![]() ,
,
此时点Q的坐标为(8,![]() );
);
②当∠GFQ=90°时,如图2所示.
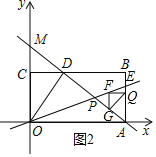
∵△FGQ为等腰直角三角形,
∴FG=FQ,即![]() t-(-t+8)=8-t,
t-(-t+8)=8-t,
解得:t=![]() ,
,
此时点Q的坐标为(8,![]() );
);
③当∠FQG=90°时,过点Q作QS⊥FG于点S,如图3所示.
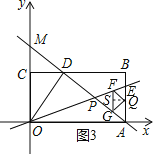
∵△FGQ为等腰直角三角形,
∴FG=2QS,即![]() t-(-t+8)=2(8-t),
t-(-t+8)=2(8-t),
解得:t=![]() ,
,
此时点F的坐标为(![]() ,4),点G的坐标为(
,4),点G的坐标为(![]() ,
,![]() )
)
此时点Q的坐标为(8,![]() ).
).
综上所述:在线段AE上存在一点Q,使得△FGQ为等腰直角三角形,当t=![]() 时点Q的坐标为(8,
时点Q的坐标为(8,![]() )或(8,
)或(8,![]() ),当t=
),当t=![]() 时点Q的坐标为(8,
时点Q的坐标为(8,![]() ).
).


科目:初中数学 来源: 题型:
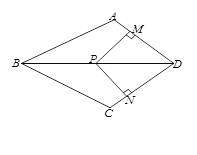
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC, P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
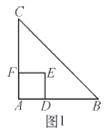
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
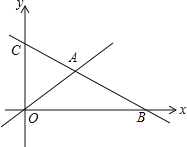
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴,y轴交于点B,C且与直线y=
x+6分别与x轴,y轴交于点B,C且与直线y=![]() x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车以![]() 匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以
匀速行驶的耗油情况,进行了试验:该轿车油箱加满后,以![]() 的速度匀速行驶,数据记录如下表:
的速度匀速行驶,数据记录如下表:
轿车行驶的路程 | 0 | 100 | 200 | 300 | … |
油箱剩余油量 | 50 | 41 | 32 | 23 | … |
(1)上表反映了哪两个变量之间的关系?自变量、因变量各是什么?
(2)油箱剩余油量![]() (升)与轿车行驶的路程
(升)与轿车行驶的路程![]() (千米)之间的关系式是什么?
(千米)之间的关系式是什么?
(3)若小明将油箱加满后,驾驶该轿车以![]() 的速度匀速从
的速度匀速从![]() 地驶往
地驶往![]() 地,到达
地,到达![]() 地时油箱剩余油量为5升,求两地之间的距离.
地时油箱剩余油量为5升,求两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
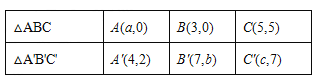
【题目】已知△A'B'C'是由△ABC经过平移得到的,它们的顶点在平面直角坐标系中的坐标如下表所示:
(1)观察表中各对应点坐标的变化,并填空:
a= , b= ,c= ;
(2)在平面直角坐标系中画出△ABC及平移后的△A'B'C';(3)△A'B'C'的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com