
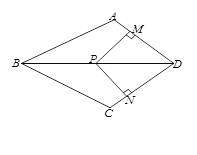
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC, P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中
AB=CB
∠ABD=∠CBD
BD=BD
∴△ABD≌△CBD(SAS)
∴∠ADB=∠CDB
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°,
∴PM=MD,
∴四边形MPND是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:(1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB
___A1B1;
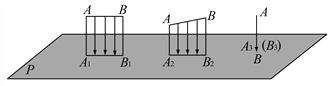
(2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB___A2B2;
(3)当线段AB垂直于投影面P时,它的正投影是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°则下列结论正确的有( )
(1)∠C′EF=32°(2)∠AEC=116°(3)∠BGE=64°(4)∠BFD=116°.

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
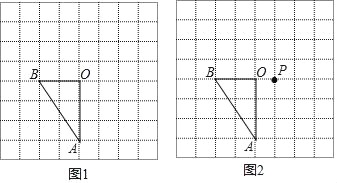
【题目】在8×8的正方形网格中,有一个Rt△AOB,点O是直角顶点,点O、A、B分别在网格中小正方形的顶点上,请按照下面要求在所给的网格中画图.
(1)在图1中,将△AOB先向右平移3个单位,再向上平移2个单位,得到△A1O1B1,画出平移后的△A1O1B1;(其中点A、O、B的对应点分别为点A1,O1,B1)
(2)在图2中,△AOB与△A2O2B2是关于点P对称的图形,画出△A2O2B2,连接BA2,并直接写出tan∠A2BO的值.(其中A,O,B的对应点分别为点A2,O2,B2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】众所周知,水的污染越来越严重,日益影响着人类的身心健康,而人们的安全饮水意识仍有待提高.已知某品牌型号Ⅰ净水器的市场售价为2000元/台,型号Ⅱ净水器的市场售价为1800元/台.为了保护我区市民的安全饮水,推动北碚区创建国家级卫生区复审工作,启动了“安全饮水北碚行”活动,此两种型号的净水器可获得13%的财政补贴.
(1)某商场在启动活动前一个月共售出此两种净水器960台,启动活动后的第一个月型号Ⅰ和型号Ⅱ净水器的销量分别比上月增长30%、25%,这个月这两种净水器共售出1228台.启动活动前一个月此两种型号的净水器销量各为多少台?
(2)在启动活动前区政府打算用25000元为天府镇敬老院购买该两种型号的净水器,并计划恰好全部用完此款.
①原计划所购买的型号Ⅰ和型号Ⅱ净水器各多少台?
②活动启动后,在不增加区政府实际负担的情况下,能否多购买两台型号Ⅱ净水器?
查看答案和解析>>
科目:初中数学 来源: 题型:
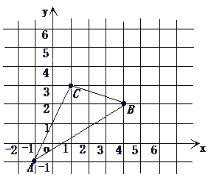
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标.
(2)求出△ABC的面积.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置。
查看答案和解析>>
科目:初中数学 来源: 题型:
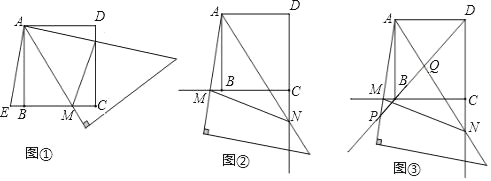
【题目】已知等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕A点旋转时,两边分别交直线BC,CD于点M、N.
(1)如图①,当M、N分别在边BC,CD上时,作AE垂直于AN,交CB的延长线于点E,求证:△ABE≌△ADN;
(2)如图②,当M、N分别在边CB,DC的延长线上时,求证:MN+BM=DN;
(3)如图③,当M、N分别在边CB,DC的延长线上时,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
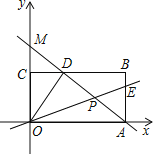
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com