
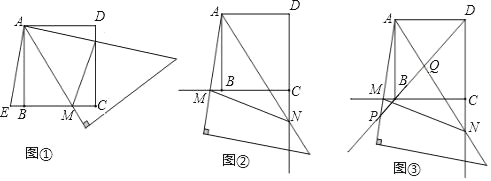
【题目】已知等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕A点旋转时,两边分别交直线BC,CD于点M、N.
(1)如图①,当M、N分别在边BC,CD上时,作AE垂直于AN,交CB的延长线于点E,求证:△ABE≌△ADN;
(2)如图②,当M、N分别在边CB,DC的延长线上时,求证:MN+BM=DN;
(3)如图③,当M、N分别在边CB,DC的延长线上时,作直线BD交直线AM、AN于P、Q两点,若MN=10,CM=8,求AP的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:![]() 由同角的余角相等得到一对锐角相等,再由一对直角相等,又正方形的边长相等,利用ASA即可得到
由同角的余角相等得到一对锐角相等,再由一对直角相等,又正方形的边长相等,利用ASA即可得到![]() ≌
≌![]()
![]() 在
在![]() 上截取
上截取![]() 连接
连接![]() 首先证明
首先证明![]() ≌
≌![]() 再证
再证![]() 为等腰直角三角形,即可得到结论;
为等腰直角三角形,即可得到结论;
![]() 连接AC,在
连接AC,在![]() 中,由MN和CM的长,利用勾股定理求出CN的长,根据图3的结论等量代换即可求出BC的长,从而利用勾股定理求出AC的长,证明
中,由MN和CM的长,利用勾股定理求出CN的长,根据图3的结论等量代换即可求出BC的长,从而利用勾股定理求出AC的长,证明![]() 且相似比为
且相似比为![]() 在
在![]() 中,利用勾股定理求出AN的长,代入比例式即可求出AP的长.
中,利用勾股定理求出AN的长,代入比例式即可求出AP的长.
试题解析:![]() 如图1,
如图1,
∵AE垂直于AN,
![]()
∵四边形ABCD是正方形,
![]() ,
,
![]()
![]()
又![]()
∴![]() ≌
≌![]() (ASA);
(ASA);
(2)证明:如图②,在![]() 上截取
上截取![]() 连接
连接![]()
![]()
![]()
∴![]() ≌
≌![]()
![]()
![]()
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,
![]()
∴AN为MG的垂直平分线,
![]()
![]() ,即
,即![]()
(3)如图③,连接AC,同(2),证得
![]()
![]()
![]()
即![]()
即![]() ,
,
在![]() 中,
中,
根据勾股定理得![]() 即
即![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
在![]() 中,
中,
根据勾股定理得![]()
解得![]()
![]()
![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC.
(1)求证:△BDG≌△ADC.
(2)分别取BG、AC的中点E、F,连接DE、DF,则DE与DF有何关系,并说明理由.
(3)在(2)的条件下,连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
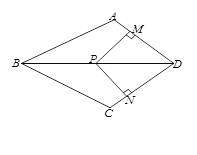
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC, P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M、N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年大豆和小麦的总产量为200吨,今年大豆和小麦的总产量为225吨,其中大豆比去年増产5%,小麦比去年増产15%,求该农场今年大豆和小麦的产量各是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG.

(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
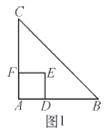
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
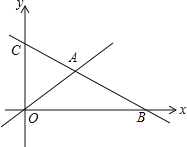
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴,y轴交于点B,C且与直线y=
x+6分别与x轴,y轴交于点B,C且与直线y=![]() x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
x+4的图象分别与x轴,y轴的正半轴交于点E、F,一次函数y=kx﹣4的图象与直线EF交于点A(m,2),且交于x轴于点P,
(1)求m的值及点E、F的坐标;
(2)求△APE的面积;
(3)若B点是x轴上的动点,问在直线EF上,是否存在点Q(Q与A不重合),使△BEQ与△APE全等?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com