
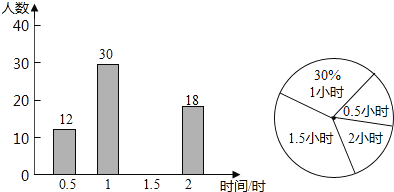
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
【答案】(1)补全的条形统计图如图所示,见解析,被调查的学生周末阅读时间的众数是1.5小时,中位数是1.5小时;(2)所有被调查学生阅读时间的平均数为1.32小时;(3)估计周末阅读时间不低于1.5小时的人数为290人.
【解析】
(1)根据统计图可以求得本次调查的学生数,从而可以求得阅读时间1.5小时的学生数,进而可以将条形统计图补充完整;由补全的条形统计图可以得到抽查的学生周末阅读时间的众数、中位数.
(2)根据补全的条形统计图可以求得所有被调查学生阅读时间的平均数.
(3)用总人数乘以样本中周末阅读时间不低于1.5小时的人数占总人数的比例即可得.
解:(1)由题意可得,本次调查的学生数为:30÷30%=100,
阅读时间1.5小时的学生数为:100﹣12﹣30﹣18=40,
补全的条形统计图如图所示,
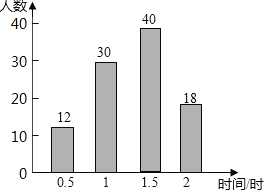
由补全的条形统计图可知,被调查的学生周末阅读时间众数是1.5小时,中位数是1.5小时,
故答案为:1.5,1.5;
(2)所有被调查学生阅读时间的平均数为:![]() ×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
×(12×0.5+30×1+40×1.5+18×2)=1.32小时,
即所有被调查同学的平均阅读时间为1.32小时.
(3)估计周末阅读时间不低于1.5小时的人数为500×![]() =290(人).
=290(人).
故答案为:(1)补全的条形统计图如图所示,见解析,被调查的学生周末阅读时间的众数是1.5小时,中位数是1.5小时;(2)所有被调查学生阅读时间的平均数为1.32小时;(3)估计周末阅读时间不低于1.5小时的人数为290人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在4×5网格图中,其中每个小正方形边长均为1,梯形ABCD和五边形EFGHK的顶点均为小正方形的顶点.
(1)以B为位似中心,在网格图中作四边形A′BC′D′,使四边形A′BC′D′和梯形ABCD位似,且位似比为2:1;
(2)求(1)中四边形A′BC′D′与五边形EFGHK重叠部分的周长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场去年大豆和小麦的总产量为200吨,今年大豆和小麦的总产量为225吨,其中大豆比去年増产5%,小麦比去年増产15%,求该农场今年大豆和小麦的产量各是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
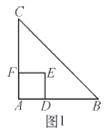
【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF; ②当AB=4,AD=![]() 时,求线段BG的长.
时,求线段BG的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入2400元;
营业员B:月销售件数300件,月总收入2700元;
假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值;
的值;
(2)若某营业员的月总收入不低于3100元,那么他当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需350元;如果购买甲1件,乙2件,丙3件共需370元.某顾客想购买甲、乙、丙各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
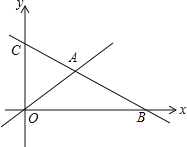
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+6分别与x轴,y轴交于点B,C且与直线y=
x+6分别与x轴,y轴交于点B,C且与直线y=![]() x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
x交于点A,点D是直线OA上的点,当△ACD为直角三角形时,则点D的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(﹣3,2).
(1)直接写出点E的坐标 ;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t= 秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,试问 x,y,z之间的数量关系能否确定?若能,请用含x,y的式子表示z,写出过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行2000米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com