
 均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形
均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形 的边长为2011,则点B2的坐标为
的边长为2011,则点B2的坐标为 
 的边长为2011,∴B2的坐标为(m,n-2011),A2的坐标为(m+2011,n-2011),∵点A2在直线OM上,则m+2011=n-2011,则n=m+4022,∴2m=m+4022,解得m=4022,则点B2的坐标为(4022,6033).故答案为:(4022,6033).
的边长为2011,∴B2的坐标为(m,n-2011),A2的坐标为(m+2011,n-2011),∵点A2在直线OM上,则m+2011=n-2011,则n=m+4022,∴2m=m+4022,解得m=4022,则点B2的坐标为(4022,6033).故答案为:(4022,6033).

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
 >20)之间的函数关系式;
>20)之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
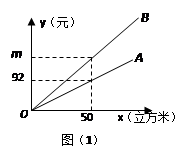
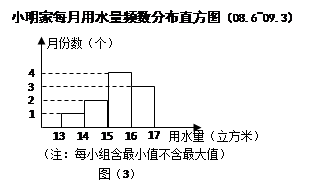
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题



查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
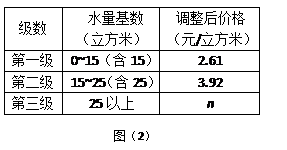
| 原收费标准 | 新按月分段收费标准 |
| 每吨2元 | (1)每月用水不超过10吨(包括10吨)的用户,每吨收费1.6元; (2)每月用水超过10吨的用户,其中的10吨按每吨1.6元收费,超过10吨的部分,按每吨 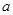 元收费( 元收费(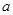 >1.6). >1.6). |
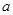 的值;
的值;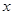 (吨),应交水费
(吨),应交水费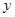 (元),求
(元),求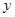 与
与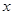 之间的函数关系式,并注明自变量x的取值范围;
之间的函数关系式,并注明自变量x的取值范围;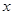 (吨)在什么范围内时,按新分段收费标准交的水费少于按原收费标准交的水费?
(吨)在什么范围内时,按新分段收费标准交的水费少于按原收费标准交的水费?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
x的图象于点B.矩形CDEF的边DC在x轴上,D在C的左侧,EF在x轴上方,DC=2,DE=4.当点C坐标为(-2,0)时,矩形CDEF开始以每秒2个单位的速度沿x轴向右运动,运动时间为t秒.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com