
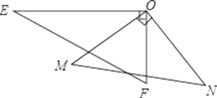
【题目】如图,一副三角板的两个直角顶点重合在一起.
(1)若∠EON=110°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
【答案】(1)∠MOF=70°,(2)∠EOM=∠FON,(3)∠EON+∠MOF=180°.
【解析】试题分析:(1)、首先根据∠EOF=90°,∠EON=110°得出∠FON=20°,然后根据∠MON=90°,得出∠MOF的度数;(2)、根据同角的余角相等得出结论;(3)、根据∠EON+∠MOF=
∠EOM+∠MOF+∠FON+∠MOF=∠EOF+∠MON得出答案.
试题解析:(1)∵∠EOF=90°,∠EON=110°,∴∠FON=20°,∵∠MON=90°,∴∠MOF=70°,
(2)∠EOM=∠FON,
∵∠EOM+∠MOF=∠FON+∠MOF=90°,∴∠EOM=∠FON,
(3)∵∠EON+∠MOF=∠EOM+∠MOF+∠FON+∠MOF,
∴∠EON+∠MOF=∠EOF+∠MON=180°.


科目:初中数学 来源: 题型:
【题目】已知三角形三边之长能求出三角形的面积吗?
海伦公式告诉你计算的方法是:S= ![]() ,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p=
,其中S表示三角形的面积,a,b,c分别表示三边之长,p表示周长之半,即p= ![]() .
.
我国宋代数学家秦九韶提出的“三斜求积术”与这个公式基本一致,所有这个公式也叫“海伦﹣秦九韶公式”.
请你利用公式解答下列问题.
(1)在△ABC中,已知AB=5,BC=6,CA=7,求△ABC的面积;
(2)计算(1)中△ABC的BC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具经销商用1.6万元购进了一批玩具,上市后一周全部售完.该经销商又用3.4万元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该经销商两次共购进这种玩具多少套?
(2)若第一批玩具销售完后总利润率为25%,购进的第二批玩具仍以第一批的相同售价出售,则第二批玩具全部售完后,这二批玩具经销商共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
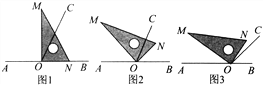
(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市中学组篮球比赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队为了争取较好名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com