

| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
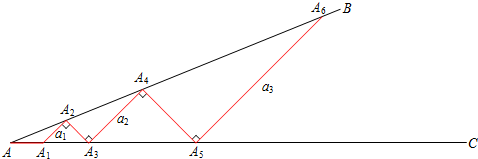
 观察猜想:我国著名的数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”说明数形结合是一种重要的数学方法,许多重要的计算转化成图形后,非常巧妙而简单,观察图形:
观察猜想:我国著名的数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非.”说明数形结合是一种重要的数学方法,许多重要的计算转化成图形后,非常巧妙而简单,观察图形:| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |
| 1 |
| 64 |
| 1 |
| 128 |
| 1 |
| 256 |
| 1 |
| 512 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 22014 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )
数学老师布置10道选择题作为课堂练习,学习委员将全班同学的答欢迎登陆全品中考网“题情况绘制成条形图,据统计图可知,答对8道题的同学的频率是( )| A、0.38 | B、0.4 |
| C、0.16 | D、0.08 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com