
 如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )
如图,一块矩形花池ABCD,AB=2$\sqrt{3}$m,AD=4m,分别以A,B,C,D为圆心,2m长为半径作四条弧交于点E,G,F,H.准备在四条弧围成的阴影区域种植紫罗兰,其余区域种植菊花,则这种紫罗兰的区域面积为( )| A. | (6$\sqrt{3}$-$\frac{4}{3}$π)m2 | B. | (8$\sqrt{3}$-$\frac{4}{3}$π)m2 | C. | (6$\sqrt{3}$-$\frac{8}{3}$π)m2 | D. | (8$\sqrt{3}$-$\frac{8}{3}$π)m2 |
分析 作GM⊥AB于M,连接AG、BG、DH,CH,先证明△ABG≌△DCH,再证明扇形的圆心角∠EAG=60°,根据种紫罗兰的区域面积=S矩形ABCD-2S△ABG-4S扇形A-EG即可计算.
解答 解: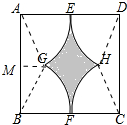 作GM⊥AB于M,连接AG、BG、DH,CH,
作GM⊥AB于M,连接AG、BG、DH,CH,
∵AG=BG=DH=CH=2,MG⊥AB,
∴AM=BM=$\sqrt{3}$,
在RT△AMG中,∵∠AMG=90°,AM=$\sqrt{3}$,AG=2,
∴MG=$\sqrt{A{G}^{2}-A{M}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
∴AG=2MG,
∴∠MAG=30°,
∵∠BAD=90°,
∴∠EAG=60°,
在△ABG和△DCH中,
$\left\{\begin{array}{l}{AB=DC}\\{AG=DH}\\{BG=CH}\end{array}\right.$,
∴△ABG≌△DCH,
∴种紫罗兰的区域面积=S矩形ABCD-2S△ABG-4S扇形A-EG=8$\sqrt{3}$-2$\sqrt{3}$-4×$\frac{60°π•{2}^{2}}{360°}$=6$\sqrt{3}$-$\frac{8π}{3}$.
故选C.
点评 本题考查扇形是面积公式、矩形的性质、勾股定理、直角三角形30°的判定等知识,解题的关键是添加辅助线利用分割法求阴影部分面积,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
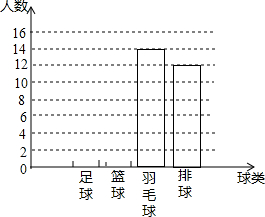 为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.
为了了解某校学生对球类运动的爱好情况,采用抽样的方法,从足球、篮球、羽毛球、排球等四个方面调查了若干名学生,并绘制成不完整的条形图.已知最喜欢篮球的人数占调查人数的32%,最喜欢排球的人数是最喜欢足球人数的1.5倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
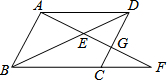 如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.
如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y<0 | B. | -3<y<-1 | C. | -6<y<-2 | D. | 2<y<6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com