练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．某实验学校成立机器人兴趣小组，他们设计了一个机器人，它能根据令进行行走和旋转，某一指令规定：机器人先向前走2米，然后向左转30°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了24米．

    分析 先判断出机器人走过的图形是正多边形，然后根据多边形的外角和等于360°求出边数，再求解即可．

    解答 解：∵机器人向前走2米，然后向左转30°，反复执行这一指令，
    ∴从出发到第一次回到原处，机器人共走过的图形是正多边形，
    边数=360°÷30°=12，
    ∴机器人共走了12×2=24米．
    故答案为：24．

    点评 本题考查了多边形的内角与外角，读懂题目信息，判断出机器人走过的图形是正多边形并求出边数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    12．如图，PA切⊙于点A，OP交⊙O于点B，且点B为OP的中点，弦AC∥OP．若OP=2，则图中阴影部分的面积为（　　）
    A．$\frac{π}{3}-\frac{{\sqrt{3}}}{2}$B．$\frac{π}{3}-\frac{{\sqrt{3}}}{4}$C．$\frac{π}{6}-\frac{{\sqrt{3}}}{2}$D．$\frac{π}{6}-\frac{{\sqrt{3}}}{4}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．已知一次函数y=kx+b的图象经过点（2，0），（1，3），则不求k，b的值，可直接得到方程kx+b=3的解是x=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，某公路隧道横截面为抛物线，其最大高度为6米，底部宽度AB长12米．
    （1）请以AB所在直线为x轴（射线AB的方向为正方向），线段AB的垂直平分线为y轴建立平面直角坐标系，求出抛物线的解析式；
    （2）若要搭建一个矩形“支架CD-DE-EF，使D、E两点在抛物线上，C、F两点在地面AB上，若AC=2米，求支架的总长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，一块矩形花池ABCD，AB=2$\sqrt{3}$m，AD=4m，分别以A，B，C，D为圆心，2m长为半径作四条弧交于点E，G，F，H．准备在四条弧围成的阴影区域种植紫罗兰，其余区域种植菊花，则这种紫罗兰的区域面积为（　　）
    A．（6$\sqrt{3}$-$\frac{4}{3}$π）m2B．（8$\sqrt{3}$-$\frac{4}{3}$π）m2C．（6$\sqrt{3}$-$\frac{8}{3}$π）m2D．（8$\sqrt{3}$-$\frac{8}{3}$π）m2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知一元二次方程的两个根2和-1，则此一元二次方程为x2-x-2=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，射线OA∥BC，BO=BC，∠OBC=50°，若将射线OA绕点O顺时针方向旋转锐角x°，射线OA恰好经过点C，则x=50．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在正方形ABCD中，AB=2，分别以点A、C为圆心，以2为半径画弧，则图中阴影部分的面积是8-2π．（结果保留π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

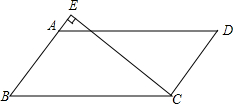    8．如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=53°，则∠BCE的度数为（　　）
    A．53°B．37°C．47°D．123°

    查看答案和解析>>

    同步练习册答案