
����Ŀ����ͼ���ڳ�����ABCD�У�AB��4cm��BE��5cm����E��AD���ϵ�һ�㣬AE��DE�ֱ�acm��bcm������(a��3)2��|2a��b��9|��0������P��B���������2cm/s���ٶ���B��C��D�˶������յ����D�����˶�ʱ��Ϊt s��
��1��a��______cm��b��______cm��
��2��tΪ��ֵʱ��EP���ı���BCDE���ܳ�ƽ�֣�
��3������һ��Q�ӵ�E����������E��D��C��·���˶������ٶ�Ϊ1cm/s����P��Q����ͬʱ������������һ�㵽���յ�ʱ����һ����ֹ֮ͣ�˶�����tΪ��ֵʱ����BPQ���������6cm2��


���𰸡���1��3��3����2��t��2s����3��t��![]() s��
s��![]() s��5s��
s��5s��
��������
��1�����ݷǸ��������ʼ������a��b��ֵ��
��2��������ı���BCDE���ܳ�������ED+DC=7��9�жϳ���P��BC�ϣ��Ӷ��õ�BP��ֵ���������ݵ�P���ٶ����ʱ�伴�ɣ�
��3���ֱ�Ե�P�͵�Q��λ�ý��з������ۣ�����0��t��3������3��t��![]() ������
������![]() ��t��5���������BPQ��������г����̼��ɽ��
��t��5���������BPQ��������г����̼��ɽ��
�⣺��1����(a��3)2��|2a��b��9|��0��
��a��3=0��2a��b��9��
��ã�a=3��b=3��
�ʴ�Ϊ��3��3��
��2��C�ı���BCDE��BC��CD��DE��EB��18cm
��EP���ı���BCDE���ܳ�ƽ�֣�
��ED+DC=7��9��
���P��BC�ϣ�
��BE+BP=9cm��
BP��4cm��
��t��![]() ��2s��
��2s��
�൱tΪ2sʱ��EP���ı���BCDE���ܳ�ƽ�֣�
��3����BC=6��ED=3��DC=4��
�൱��P���Q����ʱ��2t+t=6+3+4����ã�t=![]() s��
s��
��t=3ʱ����P�����C����Q�����D��
��t=5ʱ����P�����D�������˶�ֹͣ��
����0��t��3����P��BC�ϣ���ʱ��Q���߶�ED�ϣ���ͼ1��
��![]() ��
��
��ã�t��![]() s��
s��
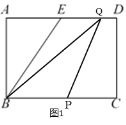
����3��t��![]() ������ǰ����ʱ��P����Q����CD�ϣ���ͼ2��
������ǰ����ʱ��P����Q����CD�ϣ���ͼ2��
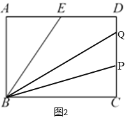
��PC=2t-6��CQ=3+4-t��
��PQ=3+4-t-(2t-6)
![]()
��ã�t��![]() s��
s��
����![]() ��t��5��������P����Q����CD�ϣ���ͼ3��
��t��5��������P����Q����CD�ϣ���ͼ3��
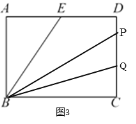
��PQ=PC-CQ=2t-6-(7-t)=3t-13��
��![]()
��ã�t��5s
�����ϣ�t��![]() s��
s��![]() s��5s��
s��5s��


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
����������˵��������ʲô���ӣ��Ҳ����ã������ҵ������ȥ�жϣ���ƽ֮��������á�����ժ�ԡ�ס���Ρ������ɫ������ҶΪ����������ɫ���١�
С��Ҹ���������һ�ι�·�����������д�ţ�������·�����������������������ðְֿ���ʻ����ι�·�������ٶ�Ϊ60ǧ�ף�Сʱ������Լ3���ӣ��ɴ˹������·��Լ_______ǧ�ס�
Ȼ��С��������ϣ���֪����Ϊ��Ҷ����ľ����������������ֱ���ɴ�8�ס�С��ƻ���·����㿪ʼ��ÿa����һ����������ʾ��ͼ���£�

���ǵ�Ͷ���ʽ�����ƣ����������һ�ַ�������ԭ�ƻ���a����һ������·������Ƽ���200�������������a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ı���ABCD�У�M��N��P��Q�ֱ���AB��BC��CD��DA�ϵĵ㣬�����ı���MNPQ����״�����½����У��������![]() ����
����![]()
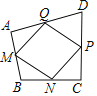
A. ��M��N��P��Q�Ǹ����е㣬�ı�MNPQһ��Ϊƽ���ı���
B. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ������
ʱ���ı���MNPQΪ������
C. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ����
ʱ���ı���MNPQΪ����
D. ��M��N��P��Q�Ǹ����е㣬��![]() ʱ���ı���MNPQΪ����
ʱ���ı���MNPQΪ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����α߳�Ϊ1�ķ���ֽ�У���ABC�Ķ��㶼�ڷ���ֽ����ϣ�����ABC����ƽ��2��������ƽ��4��
��1������ͼ�л���ƽ�ƺ�ġ�A��B��C����
��2������ͼ�л�����A��B��C���ĸ�C��D�����������ABC������ƽ�ƹ������߶�ACɨ�������Ϊ________��
��3����ʹS��MBC=S��ABC�ĸ��M����_______������M���ڵ�A��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����

��1����������ABC��CΪ��ת���ģ���˳ʱ�뷽����ת90�����ͼ����A1B1C��
��2����ԭ��OΪ�Գ����ģ��ٻ�������ABC����ԭ��O�ԳƵ���A2B2C2����д����C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��OΪ����ԭ�㣬�ı���OABCΪ���Σ�A��10��0����C��0��4������D��OA���е㣬��P�ڱ�BC����ÿ��1����λ�����ٶ��ɵ�C���B�˶���

��1����tΪ��ֵʱ���ı���PODB��ƽ���ı��Σ�
��2�����߶�PB���Ƿ����һ��Q��ʹ��ODQPΪ���Σ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
��3����OPDΪ����������ʱ��д����P�����꣨����д���̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������������̣����������������������ݣ���ͼ��

�ߡ�1+��2=180������2+��4=180��(��֪)
���1=��4( )
��c��a( )
�֡ߡ�2+��3=180��(��֪ )
��3=��6( )
���2+��6=180��( )
��a��b( )
��c��b( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���A����ǣ�EΪ��AD��һ�㣬��ABE����BE�۵���ʹ��A�Ķ�Ӧ��Fǡ�����ڱ�CD�ϣ�����EF��BF���������н��ۣ�
������A=70�㣬���ABE=35�㣻������F��CD���е㣬��S��ABE![]() S����ABCD
S����ABCD
�����ж���ȷ���ǣ�������

A. �٣��ڶ���B. �٣��ڶ���C. �ٶԣ��ڴ�D. �ٴ����ڶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˼��.
һ�죬��ʦ�ںڰ���д���������������⣺
�ٴ�ֱ��ͬһ��ֱ�ߵ�����ֱ��ƽ�У�
����![]() ����
����![]()
����![]() ��
��![]() ����������ֱ�߷ֱ�ƽ�У���
����������ֱ�߷ֱ�ƽ�У���![]() .
.
С����С���Ի����£�
С������������������⣬�������֤��.��
С������������Ǽ����⣬��������һЩ����.��
��1�����С����С���ĶԻ���̸̸��Ĺ۵�.�������Ϊ�������⣬��֤�����������Ϊ�Ǽ����⣬������һ���ʵ���������ʹ֮��������.
��2����������ڡ��������ѡһ�����������Ϊ���������⣬��֤�����������Ϊ���Ǽ����⣬��ٳ�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com