Question

【题目】如图，在任意四边形ABCD中，M，N，P，Q分别是AB，BC，CD，DA上的点，对于四边形MNPQ的形状，以下结论中，错误的是　　

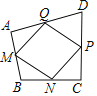
A. 当M，N，P，Q是各边中点，四边MNPQ一定为平行四边形

B. 当M，N，P，Q是各边中点，且时，四边形MNPQ为正方形

C. 当M，N、P，Q是各边中点，且时，四边形MNPQ为菱形

D. 当M，N、P、Q是各边中点，且时，四边形MNPQ为矩形

Answer 1

【答案】B

【解析】

连接AC、BD，根据三角形中位线定理得到，，，，根据平行四边形、矩形、菱形、正方形的判定定理判断即可．

解：连接AC、BD交于点O，

，N，P，Q是各边中点，

，，，，

，，

四边MNPQ一定为平行四边形，A说法正确，不符合题意；

时，四边形MNPQ不一定为正方形，B说法错误，符合题意；

时，，

四边形MNPQ为菱形，C说法正确，不符合题意；

时，，

四边形MNPQ为矩形，D说法正确，不符合题意.

故选：B．