
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 , 直线PQ与x轴所夹锐角的度数是;
(2)若两个三角形面积满足S△POQ= ![]() S△PAQ , 求m的值;
S△PAQ , 求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
【答案】
(1)2,45°
(2)解:如图

设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ= ![]() S△PAQ不成立;
S△PAQ不成立;
①当点B落在线段OA上时,如图①,

![]() =
= ![]() =
= ![]() ,
,
由△OBE∽△ABF得, ![]() =
= ![]() =
= ![]() ,
,
∴AB=3OB,
∴OB= ![]() OA,
OA,
由y=x2﹣4x得点A(4,0),
∴OB=1,
∴B(1,0),
∴1+m=0,
∴m=﹣1;
②当点B落在线段AO的延长线上时,如图②,同理可得OB= ![]() OA=2,
OA=2,

∴B(﹣2,0),
∴﹣2+m=0,
∴m=2,
综上,当m=﹣1或2时,S△POQ= ![]() S△PAQ
S△PAQ
(3)解:①过点C作CH∥x轴交直线PQ于点H,如图③,可得△CHQ是等腰三角形,
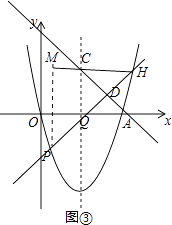
∵∠CDQ=45°+45°=90°,
∴AD⊥PH,
∴DQ=DH,
∴PD+DQ=PH,
过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,
∴PH= ![]() PM,
PM,
∴当PM最大时,PH最大,
∴当点P在抛物线顶点处时,PM最大,此时PM=6,
∴PH的最大值为6 ![]() ,
,
即PD+DQ的最大值为6 ![]() .
.
②由①可知:PD+DQ≤6 ![]() ,
,
设PD=a,则DQ ![]() ﹣a,
﹣a,
∴PDDQ≤a(6 ![]() ﹣a)=﹣a2+6
﹣a)=﹣a2+6 ![]() a=﹣(a﹣3
a=﹣(a﹣3 ![]() )2+18,
)2+18,
∵当点P在抛物线的顶点时,a=3 ![]() ,
,
∴PDDQ≤18.
∴PDDQ的最大值为18.
方法二:
⑴略.
⑵过点A作x轴垂线,与直线PQ交于点D,设直线PQ与y轴交于点C,
∴C(0,m),D(4,4+m),
∵S△POQ= ![]() (Qx﹣Px)(QY﹣CY),
(Qx﹣Px)(QY﹣CY),
S△PAQ= ![]() (Qx﹣Px)(DY﹣AY),
(Qx﹣Px)(DY﹣AY),
∵ ![]() ,
,
∴ ![]() ,
,
∴m1=2,m2=﹣1.
⑶①设P(t,t2﹣4t)(0<t<4),
∵KPQ=1,∴lPQ:y=x+t2﹣5t,
∵C(2,2),A(4,0),
∴lAC:y=﹣x+4,
∴DX= ![]() ,DY=
,DY= ![]() ,
,
∴Q(2,t2﹣5t+2),
∵PQ⊥AC,垂足为点D,
∴点Q关于直线AC的对称点Q′(﹣t2+5t+2,2),
欲使PD+DQ取得最大值,只需PQ′有最大值,
PQ′= ![]() =
= ![]() ,
,
显然当t=2时,PQ′的最大值为6 ![]() ,
,
即PD+DQ的最大值为6 ![]() ,
,
②∵(PD+DQ)2≥4PDDQ,
∴PDDQ≤ ![]() =
= ![]() =18,
=18,
∴PDDQ的最大值为18.
【解析】方法一:
解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,
∴抛物线的对称轴是x=2,
∵直线y=x+m,
∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),
∴交点到原点的距离相等,
∴直线与坐标轴围成的三角形是等腰直角三角形,
∴直线PQ与x轴所夹锐角的度数是45°,
所以答案是x=2、45°.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
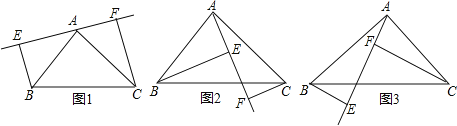
(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂。”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少。
小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树。他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约_______千米。
然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米。小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:

考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后完成.
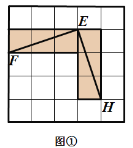
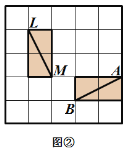
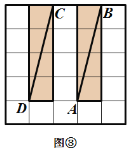
有这样一个游戏,游戏规则如下所述:如图①—图④,都是边 长为![]() 的
的![]() 网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知
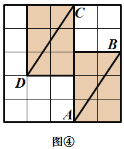
网格图,其中每条实线称为格线,格线与格线的交 点称为格点.在图①和图②中,可知![]() .在图③ 和图④中,可知
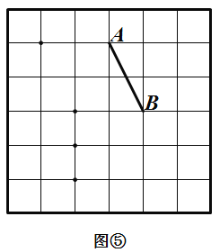
.在图③ 和图④中,可知![]() . 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的
. 根据上面的游戏规则,同学们开始闯关吧! 第一关:在图⑤的![]() 网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段
网格图中,所给各点均为格点,经过 给定的一点(不包括边框上的点),在图中画出一条与线段![]() 垂直 的线段(或者直线)
垂直 的线段(或者直线)![]() ,再画出与线段
,再画出与线段![]() 平行的一条线段(或者 直线)
平行的一条线段(或者 直线)![]() . 第二关:在图⑥的
. 第二关:在图⑥的![]() 网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)
网格图中,所给各点均为格点,经过 两对给定的点,构造两条互相垂直的直线.(在图中直接画出)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知两点A(3,0),B(0,4),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: ;
(2)求证:BM=BN;
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在任意四边形ABCD中,M,N,P,Q分别是AB,BC,CD,DA上的点,对于四边形MNPQ的形状,以下结论中,错误的是![]()
![]()
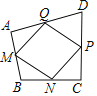
A. 当M,N,P,Q是各边中点,四边MNPQ一定为平行四边形
B. 当M,N,P,Q是各边中点,且![]() 时,四边形MNPQ为正方形
时,四边形MNPQ为正方形
C. 当M,N、P,Q是各边中点,且![]() 时,四边形MNPQ为菱形
时,四边形MNPQ为菱形
D. 当M,N、P、Q是各边中点,且![]() 时,四边形MNPQ为矩形
时,四边形MNPQ为矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.将△ABC向左平移2格,再向上平移4格.
(1)请在图中画出平移后的△A′B′C′,
(2)再在图中画出△A′B′C′的高C′D′,并求出△ABC在整个平移过程中线段AC扫过的面积为________.
(3)能使S△MBC=S△ABC的格点M共有_______个(点M异于点A)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE![]() S菱形ABCD
S菱形ABCD
下列判断正确的是( )

A. ①,②都对B. ①,②都错C. ①对,②错D. ①错,②对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com