
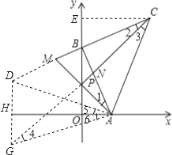
【题目】如图,在平面直角坐标系中,已知两点A(3,0),B(0,4),点C在第一象限,AB⊥BC,BC=BA,点P在线段OB上,OP=OA,AP的延长线与CB的延长线交于点M,AB与CP交于点N.

(1)点C的坐标为: ;
(2)求证:BM=BN;
(3)设点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,求证:D,G关于x轴对称.
【答案】(1)(4,7)(2)见解析(3)见解析
【解析】
(1)过点C作CE⊥y轴于点E,根据AAS证明△AOB≌△BEC,根据全等三角形的性质即可得到点C的坐标;
(2)根据全等三角形的性质和等量替换可得∠1=∠2,根据ASA证明△ABM≌△CBN,即可证得BM=BN;
(3)根据SAS证明△DAH≌△GAH,根据全等三角形的性质即可求解.
(1)过点C作CE⊥y轴于点E,故∠BEC=90°,
∴∠BEC=∠AOB,
∴∠ABC=90°,
∴∠ABO+∠CBE=90°,
∵∠ABO+∠BAO=90°
∴∠CBE=∠BAO
∴△AOB≌△BEC(AAS)
∴CE=OB=4,BE=OA=3,
∴OE=OB+BE=7,
∴C点坐标为(4,7)
(2)∵△AOB≌△BEC
∴BE=OA=OP,CE=BO,
∴PE=OB=CE,
∴∠EPC=45°,∠APC=90°,
∴∠1=∠2,
∴△ABM≌△CBN(ASA)
∴BM=BN,
(3)点C关于直线AB的对称点为D,点C关于直线AP的对称点为G,
∴AD=AC,AG=AC,
∴AD=AG,
∵∠1=∠5,∠1=∠6,
∴∠5=∠6,
在△DAH与△GAH中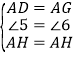
∴△DAH≌△GAH(SAS)
∴D,G关于x轴对称.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交OG于点H.
(1)求证:∠DAE=∠DCG.
(2)求线段HE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决“最后一公里”的交通接驳问题,某市投放了大量公租自行车使用,到2014年底,全市已有公租自行车25000辆,租赁点600个,预计到2016年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2014年底平均每个租赁点的公租自行车数量的1.2倍,预计到2016年底,全市将有租赁点多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
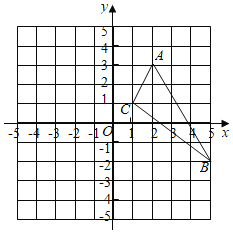
【题目】已知如图,在![]() 中,三个顶点的坐标分别为
中,三个顶点的坐标分别为![]() ,将
,将![]() 沿
沿 ![]() 轴负方向平移
轴负方向平移![]() 个单位长度,再沿
个单位长度,再沿![]() 轴负方向平移
轴负方向平移![]() 个单位长度,得到
个单位长度,得到![]() ,其 中点
,其 中点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,点
,点![]() 的对应点为点
的对应点为点![]()
![]() 直接写出平移后的
直接写出平移后的![]() 的顶点坐标:
的顶点坐标:
![]()
![]()
![]()
![]() 在坐标系中画出平移后的
在坐标系中画出平移后的![]()
![]() 求出
求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 , 直线PQ与x轴所夹锐角的度数是;
(2)若两个三角形面积满足S△POQ= ![]() S△PAQ , 求m的值;
S△PAQ , 求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: 用 2 辆![]() 型车和 1 辆
型车和 1 辆![]() 型车载满货物一次可运货 10 吨; 用 1 辆
型车载满货物一次可运货 10 吨; 用 1 辆![]() 型车和 2 辆
型车和 2 辆![]() 型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
型车载满货物一次可运货 11 吨 . 根据以上信息, 解答下列问题:
(1) 1 辆![]() 型车和 1 辆
型车和 1 辆![]() 型车载满货物一次可分别运货多少吨?
型车载满货物一次可分别运货多少吨?
(2) 某物流公司现有货物若干吨要运输, 计划同时租用![]() 型车 6 辆,
型车 6 辆,![]() 型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
型车 8 辆, 一次运完, 且恰好每辆车都满载货物, 请求出该物流公司有多少吨货物要运输?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC= ![]() ,将△ABC绕点C顺时针旋转,得到△A1B1C.
,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图①,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com