
����Ŀ����ͼ����֪��ABC�У�AB=AC����BAC=90�����ֱ��B��C����A��ֱ��EF�����ߣ�����ΪE��F��
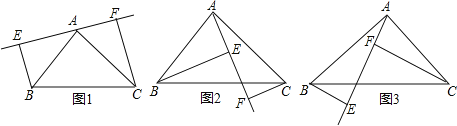
��1����ͼ1����EF��б��BC���ཻʱ����֤��EF=BE+CF��
��2����ͼ2����EF��б��BC�ཻʱ�������������䣬д��EF��BE��CF֮���������ϵ����˵�����ɣ�
��3����ͼ3������EF��BE��CF֮���ִ���������������ϵ��д�����룬����˵�����ɣ�
���𰸡���1��֤������������2) EF= BE-CF�����ɼ���������3��EF=CF-BE�����ɼ�����.
��������
��1�������BEA�ա�AFC���Ƴ�EA=FC��BE=AF�����ɵó��𰸣�
��2�������BEA�ա�AFC���Ƴ�EA=FC��BE=AF�����ɵó��𰸣�
��3�������BEA�ա�AFC���Ƴ�EA=FC��BE=AF�����ɵó��𰸣�
��1��֤������BE��EA��CF��AF��
���BAC=��BEA=��CFE=90����
���EAB+��CAF=90������EBA+��EAB=90����
���CAF=��EBA��
����ABE����CAF��
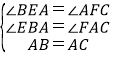
���BEA�ա�AFC��AAS����
��EA=FC��BE=AF��
��EF=EA+AF=BE+CF��
��2��֤������BE��EA��CF��AF��
���BAC=��BEA=��CFE=90����
���EAB+��CAF=90������ABE+��EAB=90����
���CAF=��ABE��
����ABE����ACF��
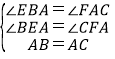
���BEA�ա�AFC��AAS����
��EA=FC��BE=AF��
��EF=AF-AE��
��EF=BE-CF��
��3��EF=CF-BE��
�����ǣ���BE��EA��CF��AF��
���BAC=��BEA=��CFA=90����
���EAB+��CAF=90������ABE+��EAB=90����
���CAF=��ABE��
����ABE����ACF��
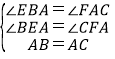 ��
��
���BEA�ա�AFC��AAS����
��EA=FC��BE=CF��
��EF=EA-AF��
��EF=CF-BE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��5��14�մ���3U863���൲�粣���ڸ߿ձ��ѣ�������Σ���ң�����Ӧ�ԣ���ȷ���ã�˳��������������һ�����ѵķ��������������纽��ʷ�ϵ��漣���±������˾������߶�������λ�õ��¶�֮��Ĵ��¹�ϵ�������±�����ش����¼������⣺
�������߶ȣ�ǧ�ף� | 0 | 1 | 2 | 3 | 4 | 5 |
����λ�õ��¶ȣ����� | 20 | 14 | 8 | 2 |
|
��1���ϱ���ӳ�����������У�______���Ա�����______�������.
��2������h��ʾ�������ĸ߶ȣ���y��ʾ��ʾ�¶ȣ���y��h��֮��Ĺ�ϵʽ�ǣ�__________��
���������߶�5ǧ��ʱ������λ�õ��¶�Ϊ��_________����
��ͼ�ǵ��շɻ��½������к��θ߶��벣�����Ѻ��������ص�������ʱ���ϵͼ������ͼ��ش��������⣺
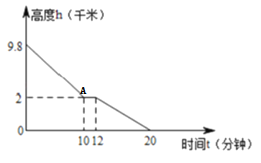
��3����A��ʾ��������ʲô������;�зɻ���2ǧ�߿�ˮƽ��Լ�����˼����ӣ�
��4���ɻ������¹�ʱ���ڸ߿յ��¶��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������ͼ1��������ABC�У�AB=AC����BAC=120������AD��BC�ڵ�D����DΪBC���е㣬��BAD=![]() ��BAC=60��������
��BAC=60��������![]() =
= ![]() =
=![]() ��
��
Ǩ��Ӧ�ã���ͼ2����ABC����ADE���ǵ��������Σ���BAC=��DAE=120����D��E��C������ͬһ��ֱ���ϣ�����BD��
����֤����ADB�ա�AEC��
����ֱ��д���߶�AD��BD��CD֮��ĵ�����ϵʽ��
��չ���죺��ͼ3��������ABCD�У���ABC=120��������ABC��������BM������C����BM�ĶԳƵ�E������AE���ӳ���BM�ڵ�F������CE��CF��
��֤����CEF�ǵȱ������Σ�
����AE=5��CE=2����BF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������^������ɽ���ز�ϲ����գ�ij���ز���˾��֯10������װ�˼ס��ҡ����������ز�ȥ������ۣ����ƻ�10������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ�����ز����ұ���װ������װ�˼������ز���������x����װ���������ز���������y���������±��ṩ����Ϣ������������⣮

��1��װ�˱������ز��ij�����Ϊ���ú�x��y��ʽ�ӱ�ʾ����
��2���ú�x��y��ʽ�ӱ�ʾ��10��������װ�����ز��Ķ�����
��3����������װ�˵��������ز�������õ��������ú�x��y��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̼ƻ���һ������Ʒ��A������B�أ��������˹�˾����·���˹�˾�����캣��Ʒ����ҵ����֪����·��Ϊ120ǧ�ף������ͻ��ٶȷֱ�Ϊ60ǧ�ף�ʱ��100ǧ�ף�ʱ�������˹�˾���շ���Ŀ���շѱ����±���ʾ��
���乤�� | ����ѵ��ۣ� (Ԫ���֡�ǧ��) | ��طѵ��ۣ� (Ԫ���֡�Сʱ) | ��·�ѣ�Ԫ | װж�������ѣ�Ԫ |
�� �� | 2 | 5 | 200 | 0 |
�� �� | 1.8 | 5 | 0 | 1600 |
ע����Ԫ���֡�ǧ�ס���ʾÿ�ֻ���ÿǧ���˷ѣ���Ԫ���֡�Сʱ����ʾÿ�ֻ���ÿСʱ����طѣ�
(1)��������̴��˵ĺ���Ʒ��x(��)���������˹�˾����·���˹�˾��Ҫ��ȡ�ķ��÷ֱ�Ϊy1(Ԫ)��y2(Ԫ)������y1��y2��x֮��ĺ�����ϵʽ��
(2)���������̴��˵ĺ���Ʒ������30�֣�Ϊ��ʡ�˷ѣ���Ӧѡ���ĸ����˹�˾�е�����ҵ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P�ӵ�A��������2cm/s���ٶ���A��C��B�˶�������B�㼴ֹͣ�˶�������P��PD��AB�ڵ�D�����˶�ʱ��Ϊx��s������ADP�����Ϊy��cm2�������ܹ���ӳy��x֮�亯����ϵ��ͼ������ǣ� ��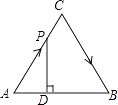
A.
B.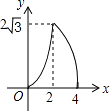
C.
D.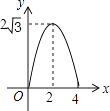
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OΪֱ��BC��һ���㣬��A��ֱ����һ���㣮��ֱ��BC��ȡ��P��ʹ����O��A��PΪ�����������Ϊ���������Σ�
(1)����AOC=30��ʱ���������ͨ���������ۡ���ͼ���Կ����ҵ����������ĵ�P����______����
(2)����ֱ��BC������ֻ���������������ĵ�P�����AOC=______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ����
��ͼ1����֪��ABCΪ�ȱ������Σ���D��E�ֱ��ڱ�AB��AC�ϣ�AD=AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲��������ͼ1�У��߶�PM��PN��������ϵ���� ������MPN�Ķ������� ����
��2��̽��֤�����ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�
���жϡ�PMN����״����˵�����ɣ�
�����MPN�Ķ�����
��3����չ����������ABCΪֱ�������Σ���BAC=90�㣬AB=AC=10����DE�ֱ��ڱ�AB��AC�ϣ�AD=AE=4������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮�ѡ�ADE�Ƶ�A��ƽ����������ת����ͼ3����ֱ��д����PMN��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2��4x��x�ύ��O��A���㣬PΪ��������һ�㣬����P��ֱ��y=x+m��Գ��ύ�ڵ�Q��
��1�����������ߵĶԳ����� �� ֱ��PQ��x��������ǵĶ�������
��2���������������������S��POQ= ![]() S��PAQ �� ��m��ֵ��
S��PAQ �� ��m��ֵ��
��3������P��x���·�����������ʱ������C��2��2����ֱ��AC��ֱ��PQ���ڵ�D����PD+DQ�����ֵ����PDDQ�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com