
 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形. ,AC=
,AC= ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D. 
 ,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得
,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得 ,所以
,所以 ,则可得
,则可得 ,再根据勾股定理的逆定理即可证得结论;②
,再根据勾股定理的逆定理即可证得结论;②
 、xy=2160可得关于x、y、z的方程组,即可求得结果;
、xy=2160可得关于x、y、z的方程组,即可求得结果; ,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得
,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得 ,所以
,所以 ,则可得
,则可得 ,再根据勾股定理的逆定理即可证得结论;②连接CE,则
,再根据勾股定理的逆定理即可证得结论;②连接CE,则 ,再根据圆周角定理可得
,再根据圆周角定理可得 ,即得BC=CE=2,
,即得BC=CE=2, ,过D作DK⊥AB于K,设KD=h,则
,过D作DK⊥AB于K,设KD=h,则 ,由
,由 ,即可求得结果.
,即可求得结果.
 代入(2)得:
代入(2)得:

 ,
,
 ,Rt△CBH中,
,Rt△CBH中,
 所以,
所以,

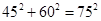 所以,△ABC是勾股三角形
所以,△ABC是勾股三角形 ,又BE是直径,所以,
,又BE是直径,所以,



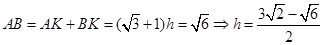

 .
.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源:不详 题型:解答题
 cm2.
cm2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的圆心在x轴上,且经过
的圆心在x轴上,且经过 、
、 两点,抛物线
两点,抛物线 (m>0)经过A、B两点,顶点为P。
(m>0)经过A、B两点,顶点为P。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com