
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: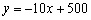 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
(1)由题意,得: w = (x-20)·y=(x-20)·(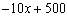 )
)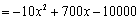 ,即
,即
w 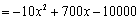 (20≤x≤32)…………(4分)
(20≤x≤32)…………(4分)
(2)对于函数w 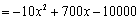 的图像的对称轴是直线
的图像的对称轴是直线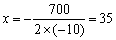 .
.
又∵a=-10<0,抛物线开口向下.∴当20≤x≤32时,W随着X的增大而增大,
∴当X=32时,W=2160 …………(8分)
答:当销售单价定为32元时,每月可获得最大利润,最大利润是2160元.
(3)取W=2000得,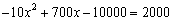 解这个方程得:x1 = 30,x2 = 40.
解这个方程得:x1 = 30,x2 = 40.
∵a=-10<0,抛物线开口向下.∴当30≤x≤40时,w≥2000.
∵20≤x≤32 ∴当30≤x≤32时,w≥2000.
设每月的成本为P(元),由题意,得: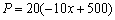
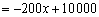
∵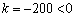 , ∴P随x的增大而减小.∴当x = 32时,P的值最小,P最小值=3600.
, ∴P随x的增大而减小.∴当x = 32时,P的值最小,P最小值=3600.
答:想要每月获得的利润不低于2000元,小明每月的成本最少为3600元.…(12分)


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
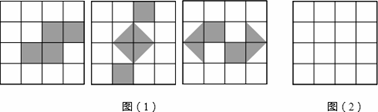
如图所示,网格中每个小正方形的边长为1,请你认真观察图(1)中的三个网格中阴影部分构成的图案,解答下列问题:
(1)这三个图案都具有以下共同特征:
①都是___对称图形;②阴影部分面积都是___;③都不是___对称图形.
(2)请你在图(2)中设计出一个具备上述特征的图案(图中已给出除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
若将函数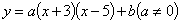 的图像向右平行移动1个单位,则它与直线
的图像向右平行移动1个单位,则它与直线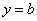 的交点坐标是( )
的交点坐标是( )
A、(-3,0)和(5,0) B、(-2,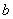 )和(6,
)和(6,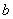 )
)
C、(-2,0)和(6,0) D、(-3,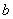 )和(5,
)和(5,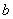 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,规定把一个正方形先沿着x轴翻折,再向右平移2个单位称为1次变换.如图,已知正方形ABCD的顶点A、B的坐标分别是(-1,-1)、(-3,-1),把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,则B的对应点B′的坐标是 .
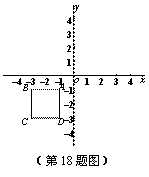
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com