
在△ABC中和△DEF中,已知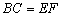 ,∠C=∠F,增加下列条件后还不能判定
,∠C=∠F,增加下列条件后还不能判定
△ABC≌△DEF的是( ).
A.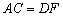 B.
B.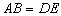
C.∠A=∠D D.∠B=∠E
科目:初中数学 来源: 题型:
阅读材料:
对于平面内的任意两点A(x1,y1),B(x2,y2),
由勾股定理易知A、B两点间的距离公式为:
AB=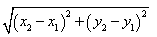 .
.
如:已知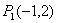 ,
,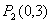 ,
,
则
解答下列问题:
已知点E(6,10),F(0,2),C(0,1)。
(1)直接应用平面内两点间距离公式计算,
E、F之间的距离为_ _5及代数式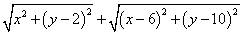 的最小值为 ;
的最小值为 ;
(2)求以C为顶点,且经过点E的抛物线的解析式;
(3)①若点D是上述抛物线上的点,且其横坐标为 -3,试求DF的长;
②若点P是该抛物线上的任意一点,试探究线段FP的长度与点P纵坐标的数量关系,并证明你的猜想。
③我们知道“圆可以看成是所有到定点的距离等于定长的点的集合”。类似地,抛物线可以看成是_______________________________________.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,菱形ABCD中,AB=2,∠C=60°,菱形ABCD在直线上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫一次操作,则经过36次这样的操作,菱形中心O所经过的路径总长为(结果保留π) .
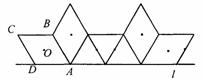
|
查看答案和解析>>
科目:初中数学 来源: 题型:
小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: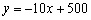 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
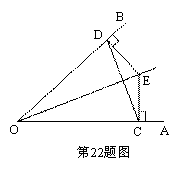
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.
求证:(1)∠EDC=∠ECD
(2)OC=OD
(3)OE是线段CD的垂直平分线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com