
解:(1)∵A(

,1),D(

+1,1),
故对称轴为直线x=
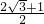
;
(2)P
1(

,1+

),P
2(

+1,1+

),P
3(

+

,1+

),
P
4(

+

,1+

);
(3)当BD与边AE垂直时,
EH=AE-AH=2-

,
∴EF=2EH=4-

,OF=2-

,
ON=
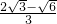
,
则F(0,

-2),N(
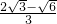
,0)
直线BD:y=

x+

-2
当BD与EA的延长线垂直时,
EK=2+

,则EG=2EK=4+

,
OG=2+

,
故直线BD:y=

x-

-2.
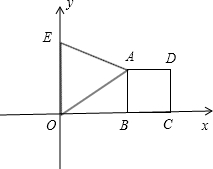
分析:(1)本题的关键是求出A、D的坐标,由于三角形OAE是等边三角形,因此直角三角形OAB中,∠AOB=30°,即AB=

OA=1,OB=

,据此可求出A、B两点的坐标,即可得出经过两点的对称轴的解析式
(2)本题有四个符合条件的点P,如图:
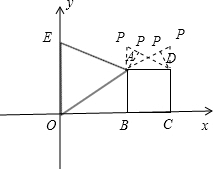
①延长OA交CD的延长线于点P,那么此时△PAD∽△AOB,在直角三角形OCP中,可根据OC的长,求出CP的长,即可得出P点坐标,那么P点关于(1)题的对称轴的对称点也符合题意,由此可求出另一个P点的坐标.
②过D作OP的垂线,设垂足为P′,那么△P′AD∽△BOA,在直角三角形APD中,过P′作AD的垂线不难求出P′点坐标,那么同①,P′关于(1)题的对称轴的对称点也符合题意,因此本题共有4个符合条件的P点.
(3)当BD与EA垂直时,有两种情况,如图:
①当BD与线段EA垂直时,那么直角三角形EHF中,∠FEH=60°,因此EF=2EH,EH的值可通过AE-AH求得,AE就是等边三角形的边长,而AH为正方形对角线的一半,据此的求出EF的长,也就求出了OF的长,同理在直角三角形OFN中,可根据OF的长和∠OFN的度数求出ON的长,即可得出F、N的坐标,用待定系数法可求出此时直线BD的解析式.
②当BD予线段EA延长线相交时,解法同①.
点评:本题考查了正方形和等边三角形的性质、图形的旋转变换等,要注意的是(2)题中,要注意以A、D、P为顶点的三角形与△AOB相似但不包括全等的条件.

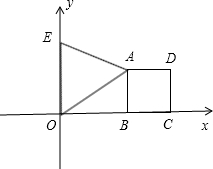 求直线BD的解析式.
求直线BD的解析式. 解:(1)∵A(
解:(1)∵A( ,1),D(
,1),D( +1,1),
+1,1),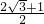 ;
; ,1+
,1+ ),P2(
),P2( +1,1+
+1,1+ ),P3(
),P3( +
+ ,1+
,1+ ),
), +
+ ,1+
,1+ );
); ,
, ,OF=2-
,OF=2- ,
,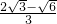 ,
, -2),N(
-2),N(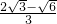 ,0)
,0) x+
x+ -2
-2 ,则EG=2EK=4+
,则EG=2EK=4+ ,
, ,
, x-
x- -2.
-2. OA=1,OB=
OA=1,OB= ,据此可求出A、B两点的坐标,即可得出经过两点的对称轴的解析式
,据此可求出A、B两点的坐标,即可得出经过两点的对称轴的解析式


 求直线BD的解析式.
求直线BD的解析式.