
����Ŀ����ƽ��ֱ������ϵ�У�������OABC�Ķ���B�ڵ�һ���ޣ�����A��C�ֱ���x���y���ϣ�ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E���Ե�EΪ�����������K������B��6��6����
��1����������K�Ľ���ʽ��
��2����P���߶�OC��һ�㣬��O����AP�ĶԳƵ�ΪM��
������M����ֱ��l1��l2��ʱ�������������»�����ƽ�ƶ��٣�ʹ�䶥������AM�ϣ�
������M�����������ϣ���ֱ��д��һ����������ĵ�P�����꣮
���𰸡�
��1����: ��ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E��
���E��������4��4����
��������K�Ľ���ʽΪy=a��x��4��2+4��
��������K������B��6��6����
��6=a��6��4��2+4��
��ã�a= ![]() ��
��
��������K�Ľ���ʽΪy= ![]() ��x��4��2+4
��x��4��2+4
��2����: ����AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2��
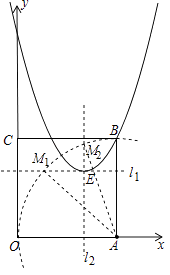
��M1��m��4����M2��4��n����
��A��6��0����OM=6��
�ࣨm��6��2+42=62����4��6��2+n2=62��
���m=6��2 ![]() ��n=4
��n=4 ![]() ��
��
��M��6��2 ![]() ��4����
��4����
�� ![]() =
= ![]() ��
��
��ã�h1= ![]() ��
��
�ཫ����������ƽ��4�� ![]() ��ʹ�䶥������AM1�ϣ�������������ƽ��4
��ʹ�䶥������AM1�ϣ�������������ƽ��4 ![]() ��4��ʹ�䶥������AM2��
��4��ʹ�䶥������AM2��
�ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
����������1�������ҳ�E������꣬���ô���ϵ����������⣻��2������AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2����M1��m��4����M2��4��n�����ɹ��ɶ����ó�����m��n�ķ��̣��ⷽ�̼��ɣ��ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
�����㾫����ͨ��������ö��κ���ͼ���ƽ�ƺ������ε����ʣ�����ƽ�Ʋ��裺��1���䷽ y=a(x-h)2+k��ȷ�����㣨h,k����2����x������Ҽ�����y���ϼ��¼����������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮


 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�ı߳�Ϊ10����M�DZ�AB��һ���㣬���ȱߡ�ABC�ع���M��ֱ���۵�����ֱ����ֱ��AC���ڵ�N��ʹ��A����ֱ��BC�ϵĵ�D������BD��DC=1��4���ۺ�ΪMN����AN�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ�����н��ۣ�
��abc��0����2a��b��0����4a��2b+c��0����4ac��b2
������ȷ�ĸ����У� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y= ![]() ��x��0��ͼ����һ��P�ĺ�������4������P��ֱ��l��x���ڵ�A����y�Ḻ�����ڵ�B����OA=OB��
��x��0��ͼ����һ��P�ĺ�������4������P��ֱ��l��x���ڵ�A����y�Ḻ�����ڵ�B����OA=OB��
��1����ֱ��l�ĺ�������ʽ��
��2������P��ֱ��l�Ĵ���l1 �� ������y= ![]() ��x��0��ͼ���ڵ�C�����OPC�������
��x��0��ͼ���ڵ�C�����OPC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��һ���ƽ������궾ƷԤ��������6.27�����̣���ʵ��߹��������ʶ�����������ܶ�����ʶ�����������и߶�����ȫ�����������֪ʶ����������ijУ���꼶ѧ����֪ʶ�����ɼ����������²�������ͳ��ͼ����

��������Ϣ������������⣺
��1��a= ��b= ��
��2�������C����������ͳ��ͼ�е�Բ�ĽǵĶ�����
��3����ȫ֪ʶ�����ɼ�Ƶ���ֲ�ֱ��ͼ��
��4����֪�������꼶��180000��ѧ���������ȫ�����꼶֪ʶ�����ɼ�����80�ֵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�꣬�ȿ��Կ��������ĶԳ�ͼ���ֿ��Կ�������Գ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��˫��11���ڼ䣬���и����̳�����������мס��ҡ��������̳���չ�Ĵ�������±���ʾ��

�������ϻ��Ϣ������������⣺
��1�������̳���ͬʱ����һ�ף�һ�����º�һ������Ϊһ�ף�ͬ���ҡ�ͬ���ϡ�ͬ��ʽ�ķ�װ���������±�۶�Ϊ290Ԫ�����ӱ�۶�Ϊ270Ԫ���Լ��������̳��ֱ��մ�������۳���һ��װ���ۼ��Ƕ���Ԫ��
��2�������������ڼס����̳�ͬʱ����һ�����380Ԫ�����º�һ�����300��Ԫ�Ŀ��ӣ�����Ҳһ���������������ӵı���Ƕ���Ԫ��
��3�����ij��Ʒ�Ƶİ������������̳��ı�۶���5Ԫ��![]() ,��̽�����Ƿ���ڷֱ��������̳���ͬ�����һ�ٶ�Ԫ�����Ҷ��ܹ�����ͬ������ͬƷ�Ƶĸô����������ֱ��˵�������̳��ù���ķ�������ָ���������̳�����������Ƕ���
,��̽�����Ƿ���ڷֱ��������̳���ͬ�����һ�ٶ�Ԫ�����Ҷ��ܹ�����ͬ������ͬƷ�Ƶĸô����������ֱ��˵�������̳��ù���ķ�������ָ���������̳�����������Ƕ���![]() ��֧���ķ����Ƕ���Ԫ���������������ֱ�ӻش�������������
��֧���ķ����Ƕ���Ԫ���������������ֱ�ӻش�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�����������ѧ���ؾ��ص�������������¡������������һ���⣺������ɳ��һ�飬����б������Сб�����бʮ�����бʮ�����֪Ϊ�X�Σ�������⽲���ǣ���һ��������ɳ������߳��ֱ�Ϊ5�12�13������ɳ������ж���������������ҹ����Ƴ��ȵ�λ��1��=500�ף����ɳ������Ϊ��������
A. 7.5ƽ��ǧ�� B. 15ƽ��ǧ�� C. 75ƽ��ǧ�� D. 750ƽ��ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
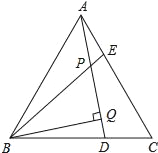
����Ŀ����֪����ͼ����ABCΪ�ȱ������Σ�AE=CD��AD��BE�ཻ�ڵ�P��BQ��AD��Q����֤��PQ=![]() BP��
BP��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com