
���� ��1����ԭʽ��Ϊm2-4mn+4n2-n2��������ƽ���ʽ������ʽ�ֽ⼴�ɣ�
��2����ԭʽ��Ϊ��m-2��2+2011����ʽ������ƽ���ķǸ��������Сֵ��
��� �⣺��1��m2-4mn+3n2=m2-4mn+4n2-n2=��m-2n��2-n2=��m-n����m-3n����
��2��m2-4m+2015=m2-4m+4+2011=��m-2��2+2011��
�ߣ�m-2��2��0��
�ࣨm-2��2+2011��2011��
�൱m=2ʱ��m2-4m+2015����Сֵ��2011��
���� ���⿼������䷽������������ϵ��Ϊ1����������һ����ϵ����һ���ƽ������������ϵ����Ϊ1���������ȡ������ϵ�������仯Ϊ1���ٽ����䷽��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{x}$+$\sqrt{2x}$=$\sqrt{3x}$ | B�� | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C�� | 2+$\sqrt{5}$=2$\sqrt{5}$ | D�� | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
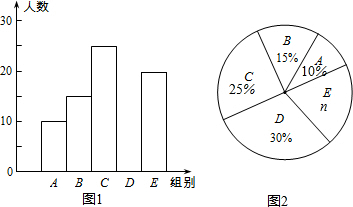
| ��� | ��ȷ����x | ���� |
| A | 0��x��8 | 10 |
| B | 8��x��16 | 15 |
| C | 16��x��24 | 25 |
| D | 24��x��32 | m |
| E | 32��x��40 | 20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{6}$ | B�� | $\sqrt{8}$=3$\sqrt{2}$ | C�� | $\sqrt{2}$��$\sqrt{3}$=$\sqrt{6}$ | D�� | $\sqrt{4}$��$\sqrt{2}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6�� | B�� | 7�� | C�� | 8�� | D�� | 9�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С�������ų�����ֽƬ��ͼ��ʾ�ڷţ�ʹС������ֽƬ��һ�������������ڴ���ֽƬ�ı��ϣ���á�1=35�㣬���2=55�㣮
С�������ų�����ֽƬ��ͼ��ʾ�ڷţ�ʹС������ֽƬ��һ�������������ڴ���ֽƬ�ı��ϣ���á�1=35�㣬���2=55�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -m2+4 | B�� | -x2-y2 | C�� | x2y2-1 | D�� | ��m+n��2-��a+b��2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com