
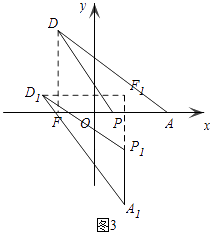
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœþy=ax2+bx+c∑÷±Ωªx÷·”⁄A£®4£¨0£©°¢B£®©Å1£¨0£©£¨Ωªy÷·”⁄µ„C£®0£¨©Å3£©£¨π˝µ„Aµƒ÷±œþy=©Å ![]() x+3Ωª≈◊ŒÔœþ”⁄¡Ì“ªµ„D£Æ
x+3Ωª≈◊ŒÔœþ”⁄¡Ì“ªµ„D£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞µ„Dµƒ◊¯±Í£ª
£®2£©»Ùµ„PŒªx÷·…œµƒ“ª∏ˆ∂ص„£¨µ„Q‘⁄œþ∂ŒAC…œ£¨«“QµΩx÷·µƒæý¿ÎŒ™ ![]() £¨¡¨Ω”PC°¢PQ£¨µ±°˜PCQµƒ÷Ð≥§◊Ó–° ±£¨«Û≥ˆµ„Pµƒ◊¯±Í£ª
£¨¡¨Ω”PC°¢PQ£¨µ±°˜PCQµƒ÷Ð≥§◊Ó–° ±£¨«Û≥ˆµ„Pµƒ◊¯±Í£ª
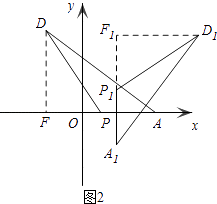
£®3£©»ÁÕº2£¨‘⁄£®2£©µƒΩ·¬€œ¬£¨¡¨Ω”PD£¨‘⁄∆Ω√ʃ⁄ «∑ҥʑ⁄°˜A1P1D1 £¨ π°˜A1P1D1°’°˜APD£®µ„A1°¢P1°¢D1µƒ∂‘”¶µ„∑÷± «A°¢P°¢D£¨A1P1∆Ω––”⁄y÷·£¨µ„P1‘⁄µ„A1…œ∑Ω£©£¨«“°˜A1P1D1µƒ¡Ω∏ˆ∂•µ„«°∫√¬‰‘⁄≈◊ŒÔœþ…œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆµ„A1µƒ∫·◊¯±Ím£¨»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø
£®1£©
Ω‚£∫°þ≈◊ŒÔœþæ≠π˝A£®4£¨0£©∫ÕB£®©Å1£¨0£©£¨
…Ë≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a£®x©Å4£©£®x+1£©£¨
∞—C£®0£¨©Å3£©¥˙»Îy=a£®x©Å4£©£®x+1£©£¨
°ý©Å3=©Å4a£¨
°ýa= ![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y= ![]() £®x©Å4£©£®x+1£©=
£®x©Å4£©£®x+1£©= ![]() x2©Å
x2©Å ![]() x©Å3£¨
x©Å3£¨
¡™¡¢ 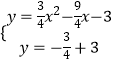 £¨
£¨
Ω‚µ√£∫x=©Å2ªÚx=4£®…·»•£©£¨
∞—x=©Å2¥˙»Îy=©Å ![]() x+3£¨
x+3£¨
y= ![]() £¨
£¨
°ýDµƒ◊¯±ÍŒ™£®©Å2£¨ ![]() £©£ª
£©£ª
£®2£©
Ω‚£∫“™ π°˜PCQµƒ÷Ð≥§◊Ó–°£¨
º¥÷ª–Ë“™PC+PQ◊Ó–°£¨
”…“‚÷™£∫QµΩx÷·µƒæý¿ÎŒ™ ![]() £¨
£¨
º¥µ„Qµƒ◊ð◊¯±ÍŒ™©Å ![]() £¨
£¨
…Ë÷±œþACµƒΩ‚Œˆ ΩŒ™y=k1x+b1£¨
∞—A£®4£¨0£©∫ÕC£®0£¨©Å3£©¥˙»Îy=k1x+b1£¨
°ý ![]() £¨
£¨
Ω‚µ√£∫ 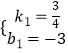 £¨
£¨
°ý÷±œþACµƒΩ‚Œˆ ΩŒ™y= ![]() x©Å3£¨
x©Å3£¨
∞—y=©Å ![]() ¥˙»Îy=
¥˙»Îy= ![]() x©Å3£¨
x©Å3£¨
°ýx= ![]() £¨
£¨
°ýQµƒ◊¯±ÍŒ™£® ![]() £¨©Å
£¨©Å ![]() £©£¨
£©£¨
…ËCπÿ”⁄x÷·∂‘≥∆µƒµ„Œ™E£¨»ÁÕº1£¨
°ýEµƒ◊¯±ÍŒ™£®0£¨3£©£¨
…Ë÷±œþEQµƒΩ‚Œˆ ΩŒ™y=k2x+b2£¨
∞—Q£® ![]() £¨©Å
£¨©Å ![]() £©∫ÕE£®0£¨3£©¥˙»Îy=k2x+b2£¨
£©∫ÕE£®0£¨3£©¥˙»Îy=k2x+b2£¨
°ý 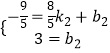 £¨
£¨
°ý ![]() £¨
£¨
°ý÷±œþEQµƒΩ‚Œˆ ΩŒ™y=©Å3x+3£¨
¡Óy=0¥˙»Îy=©Å3x+3£¨
°ýx=1£¨
°ýPµƒ◊¯±ÍŒ™£®1£¨0£© ±£¨°˜PCQµƒ÷Ð≥§◊Ó–°£ª
£®3£©
Ω‚£∫π˝µ„D◊˜DF°Õx÷·”⁄µ„F£¨
π˝µ„D1◊˜D1F1°ÕA1P1£¨ΩªA1P1µƒ—”≥§œþ”⁄µ„F1£¨
°þ°˜A1P1D1°’°˜APD£¨
°ýAF=A1F1=6£¨PF=P1F1=3£¨DF= ![]() £¨
£¨
µ±A1”ÎP1‘⁄≈◊ŒÔœþ…œ ±£¨
°þA1P1°Œy÷·£¨
°ý¥À«Èøˆ≤ª¥Ê‘⁄£ª
µ±P1”ÎD1‘⁄≈◊ŒÔœþ…œ ±£¨
°þA1µƒ∫·◊¯±ÍŒ™m£¨
°ýP1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2©Å
m2©Å ![]() m©Å3£©£¨
m©Å3£©£¨
»Ùµ„D1‘⁄÷±œþA1P1µƒ”“≤ý ±£¨»ÁÕº2£¨
¥À ±Dµƒ∫·◊¯±ÍŒ™m+ ![]() £¨
£¨
∞—x=m+ ![]() ¥˙»Îy=
¥˙»Îy= ![]() x2©Å
x2©Å ![]() x©Å3£¨
x©Å3£¨
°ýD1µƒ◊¯±ÍŒ™£®m+ ![]() £¨
£¨ ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¨
£©£¨
°ýF1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¨
£©£¨
°ýP1F1=£® ![]() m2+
m2+ ![]() m+
m+ ![]() £©©Å£®
£©©Å£® ![]() m2©Å
m2©Å ![]() m©Å3£©
m©Å3£©
= ![]() m+
m+ ![]() £¨
£¨
°ý ![]() m+
m+ ![]() =3£¨
=3£¨
°ým=©Å ![]() £¨
£¨
»Ùµ„D1‘⁄÷±œþA1P1µƒ◊Û≤ý ±£¨»ÁÕº3£¨
¥À ±Dµƒ∫·◊¯±ÍŒ™m©Å ![]() £¨
£¨
∞—x=m©Å ![]() ¥˙»Îy=
¥˙»Îy= ![]() x2©Å
x2©Å ![]() x©Å3£¨
x©Å3£¨
°ýD1µƒ◊¯±ÍŒ™£®m+ ![]() £¨
£¨ ![]() m2©Å9m+
m2©Å9m+ ![]() £©£¨
£©£¨
°ýF1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2©Å9m+
m2©Å9m+ ![]() £©£¨
£©£¨
°ýP1F1=£® ![]() m2©Å9m+
m2©Å9m+ ![]() £©©Å£®
£©©Å£® ![]() m2©Å
m2©Å ![]() m©Å3£©
m©Å3£©
=©Å ![]() m+
m+ ![]() =3£¨
=3£¨
°ým= ![]() £¨
£¨
µ±A1”ÎD1‘⁄≈◊ŒÔœþ…œ ±£¨
°þA1µƒ∫·◊¯±ÍŒ™m£¨
°ýA1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2©Å
m2©Å ![]() m©Å3£©£¨
m©Å3£©£¨
»Ùµ„D1‘⁄÷±œþA1P1µƒ”“≤ý ±£¨»ÁÕº2£¨
¥À ±Dµƒ∫·◊¯±ÍŒ™m+ ![]() £¨
£¨
∞—x=m+ ![]() ¥˙»Îy=
¥˙»Îy= ![]() x2©Å
x2©Å ![]() x©Å3£¨
x©Å3£¨
°ýD1µƒ◊¯±ÍŒ™£®m+ ![]() £¨
£¨ ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¨
£©£¨
°ýF1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2+
m2+ ![]() m+
m+ ![]() £©£¨
£©£¨
°ýA1F1=£® ![]() m2+
m2+ ![]() m+
m+ ![]() £©©Å£®
£©©Å£® ![]() m2©Å
m2©Å ![]() m©Å3£©
m©Å3£©
= ![]() m+
m+ ![]() £¨
£¨
°ý ![]() m+
m+ ![]() =6£¨
=6£¨
°ým= ![]() £¨
£¨
»Ùµ„D1‘⁄÷±œþA1P1µƒ◊Û≤ý ±£¨»ÁÕº3£¨
¥À ±Dµƒ∫·◊¯±ÍŒ™m©Å ![]() £¨
£¨
∞—x=m©Å ![]() ¥˙»Îy=
¥˙»Îy= ![]() x2©Å
x2©Å ![]() x©Å3£¨
x©Å3£¨
°ýD1µƒ◊¯±ÍŒ™£®m+ ![]() £¨
£¨ ![]() m2©Å9m+
m2©Å9m+ ![]() £©£¨
£©£¨
°ýF1µƒ◊¯±ÍŒ™£®m£¨ ![]() m2©Å9m+
m2©Å9m+ ![]() £©£¨
£©£¨
°ýA1F1=£® ![]() m2©Å9m+
m2©Å9m+ ![]() £©©Å£®
£©©Å£® ![]() m2©Å
m2©Å ![]() m©Å3£©
m©Å3£©
=©Å ![]() m+
m+ ![]() =6£¨
=6£¨
°ým=©Å ![]() £¨
£¨
◊€…œÀ˘ ˆ£¨µ±m=©Å ![]() °¢
°¢ ![]() °¢
°¢ ![]() °¢©Å
°¢©Å ![]() ±£¨ƒÐ¬˙◊„“‚£Æ
±£¨ƒÐ¬˙◊„“‚£Æ
°æΩ‚Œˆ°ø£®1£©“—÷™≈◊ŒÔœþ”Îx÷·µƒ¡Ω∏ˆΩªµ„Œ™£®4£¨0£©∫Õ£®©Å1£¨0£©£¨À˘“‘ø……Ë≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a£®x©Å4£©£®x+1£©£¨»ª∫Û∞—£®0£¨3£©¥˙»ÎΩ‚Œˆ Ωº¥ø…«Û≥ˆ≈◊ŒÔœþµƒΩ‚Œˆ Ω£¨¡™¡¢÷±œþΩ‚Œˆ Ω∫Õ≈◊ŒÔœþΩ‚Œˆ Ωº¥ø…«Û≥ˆDµƒ◊¯±Í£ª£®2£©“™«Û°˜PCQµƒ◊Ó–°÷µ£¨”…”⁄µ„Q «πÃ∂®µ„£¨À˘“‘CQ «πÃ∂®≤ª±‰µƒ£¨À˘“‘ªπ–Ë“™«Û≥ˆPC+PQ◊Ó∂ú¥ø…£¨◊˜≥ˆµ„Cπÿ”⁄x÷·µƒ∂‘≥∆µ„E£¨¡¨Ω”EQ∫Û”Îx÷·Ωª”⁄µ„P£¨¥À ±Pµ„ƒÐπª πµ√PC+PQ◊Ó∂㪣®3£©”…“‚ª≠≥ˆÕº–Œø…÷™£¨µ„D1µƒŒª÷√”–¡Ω÷÷«Èøˆ£¨“ª÷÷ «D1‘⁄÷±œþA1P1µƒ◊Û±þ£¨¡Ì“ª÷÷ «D1‘⁄÷±œþA1P1µƒ”“±þ£¨¡ÌÕ‚°˜A1P1D1µƒ¡Ω∏ˆ∂•µ„«°∫√¬‰‘⁄≈◊ŒÔœþ…œ”–»˝÷÷«Èøˆ£¨“ª «A1”ÎP1‘⁄≈◊ŒÔœþ…œ£¨∂˛ «P1”ÎD1‘⁄≈◊ŒÔœþ…œ£¨»˝ «A1”ÎD1‘⁄≈◊ŒÔœþ…œ£¨»ª∫Û∏˘æð“‚”√∫¨mµƒ Ω◊”±Ì æA1°¢P1°¢D1µƒ◊¯±Í≥ˆ¿¥£¨»ª∫Û¿˚”√»´µ»»˝Ω«–Œµƒ–‘÷ º¥ø…«Û≥ˆmµƒ÷µ£Æ
°æøºµ„æ´Œˆ°ø¿˚”√≈◊ŒÔœþ”Î◊¯±Í÷·µƒΩªµ„∂‘ƒøΩ¯––≈–∂œº¥ø…µ√µΩ¥∞∏£¨–Ë“™ Ï÷™“ª‘™∂˛¥Œ∑Ω≥õƒΩ‚ «∆‰∂‘”¶µƒ∂˛¥Œ∫Ø ˝µƒÕºœÒ”Îx÷·µƒΩªµ„◊¯±Í£Æ“Ú¥À“ª‘™∂˛¥Œ∑Ω≥Ã÷–µƒb2-4ac£¨‘⁄∂˛¥Œ∫Ø ˝÷–±Ì æÕºœÒ”Îx÷· «∑Ò”–Ωªµ„£Æµ±b2-4ac>0 ±£¨ÕºœÒ”Îx÷·”–¡Ω∏ˆΩªµ„£ªµ±b2-4ac=0 ±£¨ÕºœÒ”Îx÷·”–“ª∏ˆΩªµ„£ªµ±b2-4ac<0 ±£¨ÕºœÒ”Îx÷·√ª”–Ωªµ„£Æ


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–ŒABCD÷–£¨±þABµƒ≥§Œ™3£¨µ„E£¨F∑÷±‘⁄AD£¨BC…œ£¨¡¨Ω”BE£¨DF£¨EF£¨BD£Æ»ÙÀƒ±þ–ŒBFDE «¡‚–Œ£¨«“OE=AE£¨‘Ú±þBCµƒ≥§Œ™£® £© 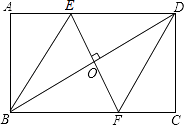
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™a «◊Ó¥Ûµƒ∏∫’˚ ˝£¨b «5µƒœý∑¥ ˝£¨c=|2|£¨«“a°¢b°¢c∑÷± «µ„A. B.C‘⁄ ˝÷·…œ∂‘”¶µƒ ˝.
(1)«Ûa°¢b°¢cµƒ÷µ£¨≤¢‘⁄ ˝÷·…œ±Í≥ˆµ„A. B. C.
(2)»Ù∂ص„P¥”µ„A≥ˆ∑¢—ÿ ˝÷·’˝∑ΩœÚ‘À∂Ø£¨∂ص„QÕ¨ ±¥”µ„B≥ˆ∑¢“≤—ÿ ˝÷·’˝∑ΩœÚ‘À∂Ø£¨µ„PµƒÀŸ∂» «√ø√Î3∏ˆµ•Œª≥§∂»£¨µ„QµƒÀŸ∂» «√ø√Î1∏ˆµ•Œª≥§∂»£¨«Û‘À∂غ∏√Î∫Û£¨µ„Qø…“‘◊∑…œµ„P?
(3)‘⁄ ˝÷·…œ’““ªµ„M£¨ πµ„MµΩA. B.C»˝µ„µƒæý¿Î÷Æ∫Õµ»”⁄12£¨«Î÷±Ω”–¥≥ˆÀ˘”–µ„M∂‘”¶µƒ ˝.
![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ“π˙∫∫¥˙ ˝—ߺ“’‘À¨Œ™¡À÷§√˜π¥π…∂®¿Ì£¨¥¥÷∆¡À“ª∑˘°∞œ“Õº°±£¨∫Û»À≥∆∆‰Œ™°∞’‘À¨œ“Õº°±£¨À¸ «”√∞À∏ˆ»´µ»µƒ÷±Ω«»˝Ω«–Œ∆¥Ω”∂¯≥…£¨º«Õº÷–’˝∑Ω–ŒABCD£¨’˝∑Ω–ŒEFGH£¨’˝∑Ω–ŒMNKTµƒ√ʪ˝∑÷±Œ™S1£¨S2£¨S3£Æ»ÙS1+S2+S3£Ω15£¨‘ÚS2µƒ÷µ «_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø÷ÿ«Ï¥Û∆∫ ±¥˙ÃÏΩ÷“—≥…Œ™»À√«÷Ѓ©–𜖔ȿ÷µƒ÷ÿ“™≥°À˘£¨ ±¥˙ÃÏΩ÷¥”“ª¬•µΩ∂˛¬•”–“ª◊‘∂Ø∑ˆÃ𣮻ÁÕº1£©£¨Õº2 «≤ý√Ê æ“‚Õº£Æ“—÷™◊‘∂Ø∑ˆÃðACµƒ∆¬∂»Œ™i=1£∫2.4£¨AC=13m£¨BE «∂˛¬•¬•∂•£¨EF°ŒMN£¨B «EF…œ¥¶‘⁄◊‘∂Ø∑ˆÃð∂•∂ÀC’˝…œ∑Ωµƒ“ªµ„£¨«“BC°ÕEF£¨‘⁄◊‘∂Ø∑ˆÃðµ◊∂ÀA¥¶≤‚µ√Bµ„—ˆΩ«Œ™42°„£Æ£®sin42°„°÷0.67£¨cos42°„°÷0.74£¨tan42°„°÷0.90£© 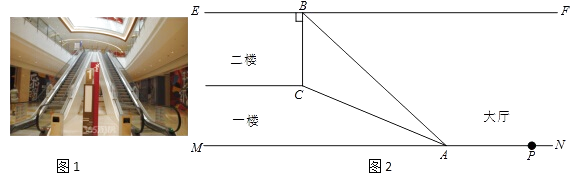
Œ™¡ÀŒ¸“˝πÀøÕ£¨ø™∑¢…ÜΑ⁄P¥¶∑≈÷√“ª∏ˆ∏þ10mµƒ°∂∑ËøÒ∂ØŒÔ≥«°∑µƒ◊∞ ŒµÒœÒ£¨≤¢“™«ÛµÒœÒ◊Ó∏þµ„”Î∂˛¬•∂•≤„“™¡Ù≥ˆ2mæý¿Î∫√∑≈÷√µ∆æþ£¨«ÎŒ ’‚∏ˆµÒœÒƒÐ∑≈µ√œ¬¬£ø»Áπ˚≤ªƒÐ£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Á…œÕºÀ˘ æ£Æ“—÷™£∫‘⁄’˝∑Ω–ŒABCD÷–£¨°œBACµƒ∆Ω∑÷œþΩªBC”⁄E£¨◊˜EF°ÕAC”⁄F£¨◊˜FG°ÕAB”⁄G£Æ‘Ú ![]() = £Æ
= £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„O «æÿ–ŒABCDµƒ÷––ƒ£¨E «AB…œµƒµ„£¨—ÿCE’€µ˛∫Û£¨µ„B«°∫√”ε„O÷ÿ∫œ£¨»ÙBC=3£¨‘Ú’€∫€CEµƒ≥§Œ™£® £© 
A.2 ![]()
B.![]()
![]()
C.![]()
D.6
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—œ¬¡–∏˜ Ω∑÷Ω‚“Ú Ω£∫
£®1£©3x©Å12x3
£®2£©£®x2+4£©2©Å16x2
£®3£©y£®y+4£©©Å4£®y+1£©
£®4£©![]()
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþl1µƒ◊Ó∏þµ„Œ™P£®3£¨4£©£¨«“æ≠π˝µ„A£®0£¨1£©£¨Ω´≈◊ŒÔœþl1»∆‘≠µ„O–˝◊™180°„∫Û£¨µ√µΩ≈◊ŒÔœþl2 £¨ «Ûl2µƒΩ‚Œˆ Ω£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com