
科目:初中数学 来源: 题型:
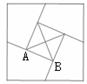
图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+4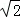 ,则图3中线段AB的长为 .
,则图3中线段AB的长为 .
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
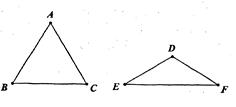
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,
则△ABC与△DEF的面积比为
A.9:4 B.3:2 C.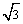 :
: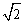 D.3
D.3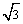 :2
:2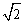
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的有 (请填写所有正确结论的序号)
①在一个装有2白球和3个红球的袋中摸3个球,摸到红球是必然事件.
②若 =-1-2a,则a≥
=-1-2a,则a≥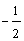 ③已知反比例函数y=-
③已知反比例函数y=-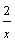 ,若x1<x2,则y1<y2
,若x1<x2,则y1<y2
④分式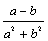 是最简分式 ⑤
是最简分式 ⑤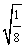 和
和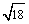 是同类二次根式
是同类二次根式
查看答案和解析>>
科目:初中数学 来源: 题型:
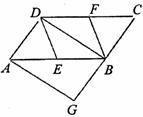
如图,□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一次函y=-2x+2,点A(-1,a),B(-2,b)在该函数图像上,则a与b的大小关系是( ).
A. a < b B. a>b C.a ≥ b D.a = b
查看答案和解析>>
科目:初中数学 来源: 题型:
已知矩形ABCD中, AB=3cm,AD=4cm,点E、F
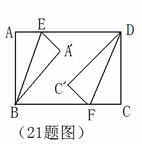
AB=3cm,AD=4cm,点E、F 分别在边AD、BC上,连接B、E,D、F.分别把RtΔBAE和RtΔDCF沿 BE,DF折叠成如图所示位置。
分别在边AD、BC上,连接B、E,D、F.分别把RtΔBAE和RtΔDCF沿 BE,DF折叠成如图所示位置。
(1)若得到四边形 BFDE是菱形,求AE的长.
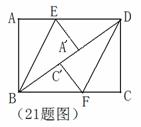
(2) 若折叠后点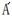 和点
和点 恰好落在
恰好落在 对角线BD上,求AE的长.
对角线BD上,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com