
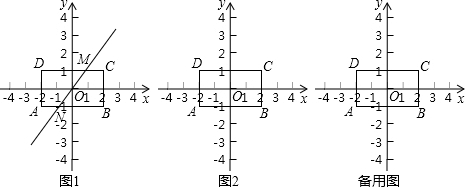
 如图,在平面直角坐标系xOy中,过点A(4,0)的直线l1与直线l2:y=-2x相交于点B(-4,m).
如图,在平面直角坐标系xOy中,过点A(4,0)的直线l1与直线l2:y=-2x相交于点B(-4,m).分析 (1)求出m=8,由待定系数法求出直线解析式即可;
(2)求出C点坐标,求出平行于l2的直线过点C时表达式为y=-2x+4,平行于l2的直线过点D时表达式为y=-2x+8,即可得出答案.
解答 解:(1)∵点B(-4,m)在直线l2:y=-2x上,
∴m=8.
∵点A(4,0)和B(-4,8)在直线l1上,设l1:y=kx+b,
∴$\left\{\begin{array}{l}4k+b=0\\-4k+b=8.\end{array}\right.$解得$\left\{\begin{array}{l}k=-1\\ b=4.\end{array}\right.$,
∴直线l1的表达式为y=-x+4.
(2)点C坐标为(0,4),
平行于l2的直线过点C时表达式为y=-2x+4,
平行于l2的直线过点D时表达式为y=-2x+8,
∴n的取值范围是 4≤n≤8.
点评 本题考查了两直线相交的问题,主要利用了待定系数法求一次函数解析式,联立两函数解析式求交点坐标,一定要熟练掌握并灵活运用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{a}$=$\frac{-1}{a}$ | B. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{a+b}$ | C. | $\frac{2{b}^{2}}{{a}^{2}}$=$\frac{2b}{a}$ | D. | $\frac{a+ab}{b+ab}$=$\frac{a}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠A=36°,∠B=60°,EF∥BC,FG平分∠AFE,则AFG的度数为( )
如图,△ABC中,∠A=36°,∠B=60°,EF∥BC,FG平分∠AFE,则AFG的度数为( )| A. | 36° | B. | 37° | C. | 42° | D. | 47° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对某校七年级一班全体同学喜爱球类运动的情况进行调查,采用抽样调查的方式 | |
| B. | 了解赤峰市九年级同学的视力情况,采用全面调查的方式 | |
| C. | 某农田保护区对区内的小麦的高度进行调查,采用全面调查的方式 | |
| D. | 对宁城县食品合格情况的调查,采用抽样调查的方式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com