Question

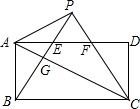
4．如图，在矩形ABCD中，AB=$\sqrt{3}$，BC=3，将△ABC沿对角线AC折叠，点B恰好落在点P处，CP与AD交于点F，连接BP交AC于点G，交AD于点E，下列结论错误的是（　　）

• A． AC=2AP
• B． △PBC是等边三角形
• C． S_△BGC=3S_△AGP
• D． $\frac{PG}{CG}$=$\frac{1}{3}$

Answer 1

分析 如图，首先运用勾股定理求出AC的长度，进而求出∠ACB=30°，此为解决该题的关键性结论；运用翻折变换的性质证明△BCP为等边三角形；运用射影定理求出线段CG、AG之间的数量关系，进而证明选项A、B、C成立，选项D不成立．

解答 解：如图，∵四边形ABCD为矩形，
∴∠ABC=90°；由勾股定理得：
AC²=AB²+BC²，而AB=$\sqrt{3}$，BC=3，
∴AC=2$\sqrt{3}$，AB=$\frac{1}{2}$AC，
∴∠ACB=30°；由翻折变换的性质得：
BP⊥AC，∠ACB=∠ACP=30°，
BC=PC，AB=AP，BG=PG，
∴GC=$\sqrt{3}$BG=$\sqrt{3}$PG，∠BCP=60°，AC=2AP，
∴△BCP为等边三角形，
故选项A、B成立，选项D不成立；
由射影定理得：BG²=CG•AG，
∴AG=$\frac{\sqrt{3}}{3}$BG，CG=3AG，
∴S_△BCG=3S_△ABG；由题意得：
S_△ABG=S_△AGP，
∴S_△BGC=3S_△AGP，
故选项C正确；
故答案为D．

点评 该题主要考查了翻折变换的性质、矩形的性质、射影定理、三角形的面积公式等几何知识点及其应用问题；
解题的关键是灵活运用矩形的性质、射影定理等几何知识点来分析、判断、推理或解答；对综合的分析问题解决问题的能力提出了较高的要求．