
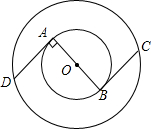
 如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=
如图,在两个同心圆⊙O中,AB是小圆的直径,BC与小圆相切于点B,并交大圆于点C,且BC=| 2 |
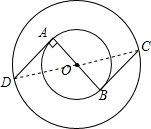 解:(1)由图形的对称性知图形是中心对称图形.
解:(1)由图形的对称性知图形是中心对称图形.| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H查看答案和解析>>
科目:初中数学 来源: 题型:
 校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.
校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=
如图,点P(0,m2)(m>0)在y轴正半轴上,过点P作平行于x轴的直线,分别交抛物线C1:y=| 1 |
| 4 |
| 1 |
| 9 |
| AB |
| CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com